Prediction of velocity and pressure of gas-liquid flow using spectrum-based physics-informed neural networks

doi:10.1007/s10483-025-3217-8

Abstract

Abstract:

This research introduces a spectrum-based physics-informed neural network (SP-PINN) model to significantly improve the accuracy of calculation of two-phase flow parameters, surpassing existing methods that have limitations in global and continuous data sampling. SP-PINNs address the challenges of traditional methods in terms of continuous sampling by integrating the spectral analysis and pressure correction into the Navier-Stokes (N-S) equations, enhancing the predictive accuracy especially in critical regions like gas-phase boundaries and velocity peaks. The novel introduction of a pressure-correction module within SP-PINNs mitigates prediction errors, achieving a substantial reduction to 1‰ compared with the conventional physics-informed neural network (PINN) approaches. Experimental applications validate the model’s ability to accurately and rapidly predict flow parameters with different sampling time intervals, with the computation time of predicting unsampled data less than 0.01 s. Such advancements signify a 100-fold improvement over traditional DNS calculations, underscoring the model’s potential in the real-time calculation and analysis of multiphase flow dynamics.

Key words: physics-informed neural network (PINN), spectral method, two-phase flow, parameter prediction

2010 MSC Number:

O359

Nanxi DING, Hengzhen FENG, H. Z. LOU, Shenghua FU, Chenglong LI, Zihao ZHANG, Wenlong MA, Zhengqian ZHANG. Prediction of velocity and pressure of gas-liquid flow using spectrum-based physics-informed neural networks. Applied Mathematics and Mechanics (English Edition), 2025, 46(2): 341-356.

TrendMD

Figures/Tables 18

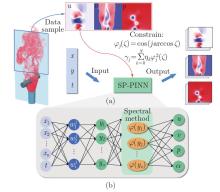
Fig. 1

Fig. 2

Fig. 3

Fig. 4

Fig. 5

Table 1

Algorithm pseudocode"

SP-PINN algorithm
Initialize neural network parameters $θ$ and $θ p$ .
Randomly set weights $(ω)$ and biases $(b)$ for the neural network.
Start the training loop with epoch $E epoch$ being 1.
While $L > L threshold$ :
	$E epoch$ := $E epoch$ + 1.
	Randomly select data from the datasets, and input them into the neural network.
	Calculate $u, v$ , and $p$ (velocity components and pressure).
	Use the obtained $u, v$ , and $p$ values as inputs to $L PDE$ .
	Calculate losses for initial conditions, boundary conditions, and observations.
	$L = ω 1 L PDE + ω 2 L init + ω 3 L boundary + ω 4 L data$ .
	Compute gradients $∇ L PDE$ , $∇ L init$ , $∇ L boundary$ , and $∇ L data$ .
	Calculate the gradient $∇ L p$ for the pressure loss function separately.
	Update neural network parameter $θ p$ using the pressure loss gradient.
	Calculate the total loss based on different weight parameters.
	Update the neural network parameter $θ$ .
End

Table 1

Fig. 6

Fig. 7

Table 2

Training parameters"

Parameter		Value
Learning rate		0.001
	Batch	32
	$E epoch$	650
	$λ 1, λ 2$	1, 1
	$L threshold$	0.002

Table 2

Fig. 8

Fig. 9

Fig. 10

Fig. 11

Fig. 12

Fig. 13

Fig. 14

Fig. 15

Fig. 16

References 26

[1]	HOSSEINI, S., TAYLAN, O., ABUSURRAH, M., AKILAN, T., NAZEMI, E., EFTEKHARI-ZADEH, E., BANO, F., and ROSHANI, G. H. Application of wavelet feature extraction and artificial neural networks for improving the performance of gas-liquid two-phase flow meters used in oil and petrochemical industries. Polymers, 13(21), 3647 (2021)
[2]	CHENG, Z. and WACHS, A. Physics-informed neural network for modelling force and torque fluctuations in a random array of bidisperse spheres. arXiv, arXiv: (2023)
[3]	XUAN, W., LOU, H., FU, S., ZHANG, Z., and DING, N. Physics-informed deep learning method for the refrigerant filling mass flow metering. Flow Measurement and Instrumentation, 93, 102418 (2023)
[4]	LI, S. and BAI, B. Gas-liquid two-phase flow rates measurement using physics-guided deep learning. International Journal of Multiphase Flow, 162, 104421 (2023)
[5]	ALIYU, A. M., CHOUDHURY, R., SOHANI, B., ATANBORI, J., RIBEIRO, J. X. F., AHMED, S. K. B., and MISHRA, R. An artificial neural network model for the prediction of entrained droplet fraction in annular gas-liquid two-phase flow in vertical pipes. International Journal of Multiphase Flow, 164, 104452 (2023)
[6]	LU, L., JIN, P., PANG, G., ZHANG, Z., and KARNIADAKIS, G. E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature Machine Intelligence, 3(3), 218–229 (2021)
[7]	LU, L., MENG, X., MAO, Z., and KARNIADAKIS, G. E. DeepXDE: a deep learning library for solving differential equations. SIAM Review, 63(1), 208–228 (2021)
[8]	LU, D. and CHRISTOV, I. C. Physics-informed neural networks for understanding shear migration of particles in viscous flow. International Journal of Multiphase Flow, 165, 104476 (2023)
[9]	CHOI, S., JUNG, I., KIM, H., NA, J., and LEE, J. M. Physics-informed deep learning for data-driven solutions of computational fluid dynamics. Korean Journal of Chemical Engineering, 39(3), 515–528 (2022)
[10]	ZHANG, R., HU, P., and MENG, Q. DRVN (deep random vortex network): a new physics-informed machine learning method for simulating and inferring incompressible fluid flows. Physics of Fluids, 34(10), 107112 (2022)
[11]	RAISSI, M., PERDIKARIS, P., and KARNIADAKIS, G. E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics, 378, 686–707 (2019)
[12]	KARNIADAKIS, G. E., KEVREKIDIS, I. G., LU, L., PERDIKARIS, P., WANG, S. F., and YANG, L. Physics-informed machine learning. Nature Reviews Physics, 3(6), 422–440 (2021)
[13]	QIU, R., HUANG, R., XIAO, Y., WANG, J. Z., ZHANG, Z., YUE, J. S., ZENG, Z., and WANG, Y. W. Physics-informed neural networks for phase-field method in two-phase flow. Physics of Fluids, 34(5), 052109 (2022)
[14]	SUN, K. and FENG, X. A second-order network structure based on gradient-enhanced physics-informed neural networks for solving parabolic partial differential equations. Entropy, 25(4), 674 (2023)
[15]	FINLAYSON, B. A. The Method of Weighted Residuals and Variational Principles, Society for Industrial and Applied Mathematics, Philadelphia (2013)
[16]	RAFIQ, M., RAFIQ, G., and CHOI, G. S. DSFA-PINN: deep spectral feature aggregation physics informed neural network. IEEE Access, 10, 22247–22259 (2022)
[17]	GOTTLIEB, D. and ORSZAG, S. A. Numerical Analysis of Spectral Methods: Theory and Applications, Society for Industrial and Applied Mathematics, Philadelphia (1977)
[18]	OUYANG, H., ZHU, Z., CHEN, K., TIAN, B., HUANG, B., and HAO, J. Reconstruction of hydrofoil cavitation flow based on the chain-style physics-informed neural network. Engineering Applications of Artificial Intelligence, 119, 105724 (2023)
[19]	MAO, Z. P. and MENG, X. H. Physics-informed neural networks with residual/gradient-based adaptive sampling methods for solving partial differential equations with sharp solutions. Applied Mathematics and Mechanics (English Edition), 44(7), 1069–1084 (2023) https://doi.org/10.1007/s10483-023-2994-7
[20]	HE, Y. C., WANG, Z. C., XIANG, H., JIANG, X. M., and TANG, D. W. An artificial viscosity augmented physics-informed neural network for incompressible flow. Applied Mathematics and Mechanics (English Edition), 44(7), 1101–1110 (2023) https://doi.org/10.1007/s10483-023-2993-9
[21]	WU, W., DANEKER, M., JOLLEY, M. A., TURNER, K. T., and LU, L. Effective data sampling strategies and boundary condition constraints of physics-informed neural networks for identifying material properties in solid mechanics. Applied Mathematics and Mechanics (English Edition), 44(7), 1039–1068 (2023) https://doi.org/10.1007/s10483-023-2995-8
[22]	NGUYEN, V. L., DEGAWA, T., UCHIYAMA, T., and TAKAMURE, K. Numerical simulation of bubbly flow around a cylinder by semi-Lagrangian-Lagrangian method. International Journal of Numerical Methods for Heat & Fluid Flow, 29(12), 4660–4683 (2019)
[23]	UCHIYAMA, T. Numerical simulation of gas-liquid two-phase flow around a rectangular cylinder by the incompressible two-fluid model. Nuclear Science and Engineering, 133(1), 92–105 (1999)
[24]	BRUNTON, S. L. and KUTZ, J. N. Promising directions of machine learning for partial differential equations. Nature Computational Science, 4(7), 483–494 (2024)
[25]	SADEQUE, M. A., RAJARATNAM, N., and LOEWEN, M. R. Flow around cylinders in open channels. Journal of Engineering Mechanics, 134(1), 60–71 (2008)
[26]	RAO, C., SUN, H., and LIU, Y. Physics-informed deep learning for incompressible laminar flows. Theoretical and Applied Mechanics Letters, 10(3), 207–212 (2020)