Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (5): 795-812.doi: https://doi.org/10.1007/s10483-025-3249-8
Previous Articles Next Articles
Tianchi YU1, Feng LIANG2,3,†(
), Hualin YANG2,3
Email Alert
RSSReceived:2025-01-15
Revised:2025-03-10
Online:2025-05-07
Published:2025-05-07
Contact:
Feng LIANG, E-mail: lf84411@163.comSupported by:2010 MSC Number:
Tianchi YU, Feng LIANG, Hualin YANG. Vibration energy harvesting of a three-directional functionally graded pipe conveying fluids. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 795-812.
Fig. 1
Schematic diagrams of the vibration energy harvester based on a 3D FG pipe conveying fluids: (a) general view; (b) cross-sectional view (color online)"
Table 1
Material parameters of the 3D FG energy harvester"
| Property | Value |
|---|---|
| Epoxy elastic modulus | 4.35 GPa |
| Epoxy density | 1 180 kg/m3 |
| Metal elastic modulus | 105 GPa |
| Metal density | 9 000 kg/m3 |
| Piezoelectric layer elastic modulus | 60.6 GPa |
| Piezoelectric layer density | 7 500 kg/m3 |
| Piezoelectric layer permittivity | 21 nF/m |
| Piezoelectric constant |
Fig. 2
Output peak voltage of a uniform bimorph pipe energy harvester with respect to the excitation frequency, where the damping ratio ξi=0.05, i=1, 2, 3, ⋯, and the load resistance R=20 kΩ (color online)"
Table 2
The first three natural frequencies of the pipe energy harvester determined by different methods"
| Natural frequency | Galerkin | COMSOL | Resonance frequency |
|---|---|---|---|
| 1st-order | 63.5 | 64.1 | 63.5 |
| 2nd-order | 397.7 | 398.2 | 396.1 |
| 3rd-order | 1 113.6 | 1 096.0 | 1 114.1 |
Fig. 3
The first three mode shapes of the pipe energy harvester obtained by FE simulation (color online)"
Fig. 4
Theoretically predicted peak voltage harvested by a bimorph cantilevered beam with a load resistance of 470 kΩ (color online)"
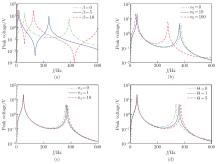
Fig. 5
Output peak voltage of the 3D FG pipe energy harvester under effects of different FGM parameters: (a) the index β, describing the gradient distribution of material properties along the axial direction of the pipe; (b) the index n2, describing the gradient distribution of material properties along the height direction of the pipe; (c) the index n1, describing the gradient distribution of material properties along the width direction of the pipe, for Θ=10; (d) the parameter Θ, a material constant in the width direction of the pipe (color online)"
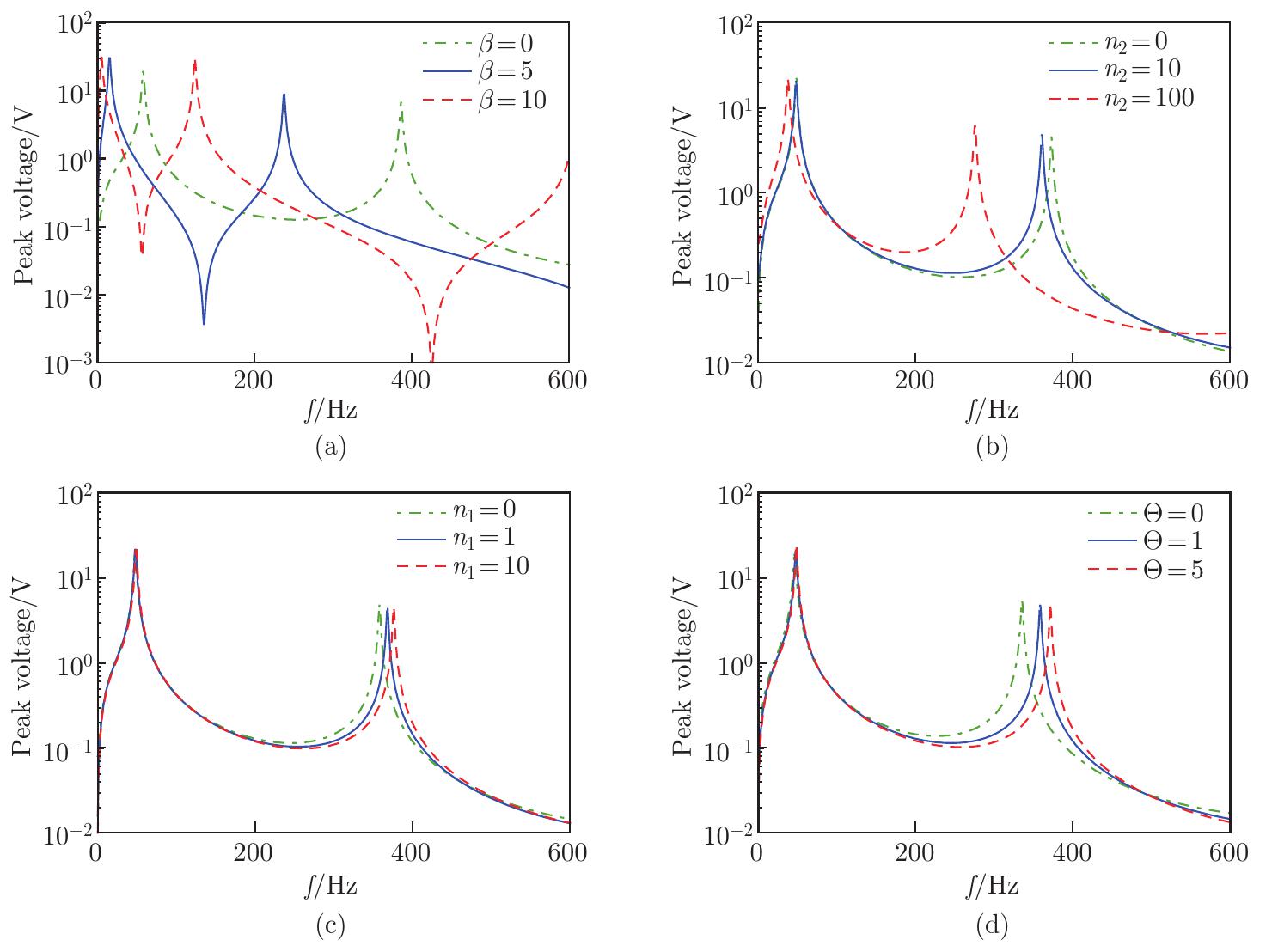
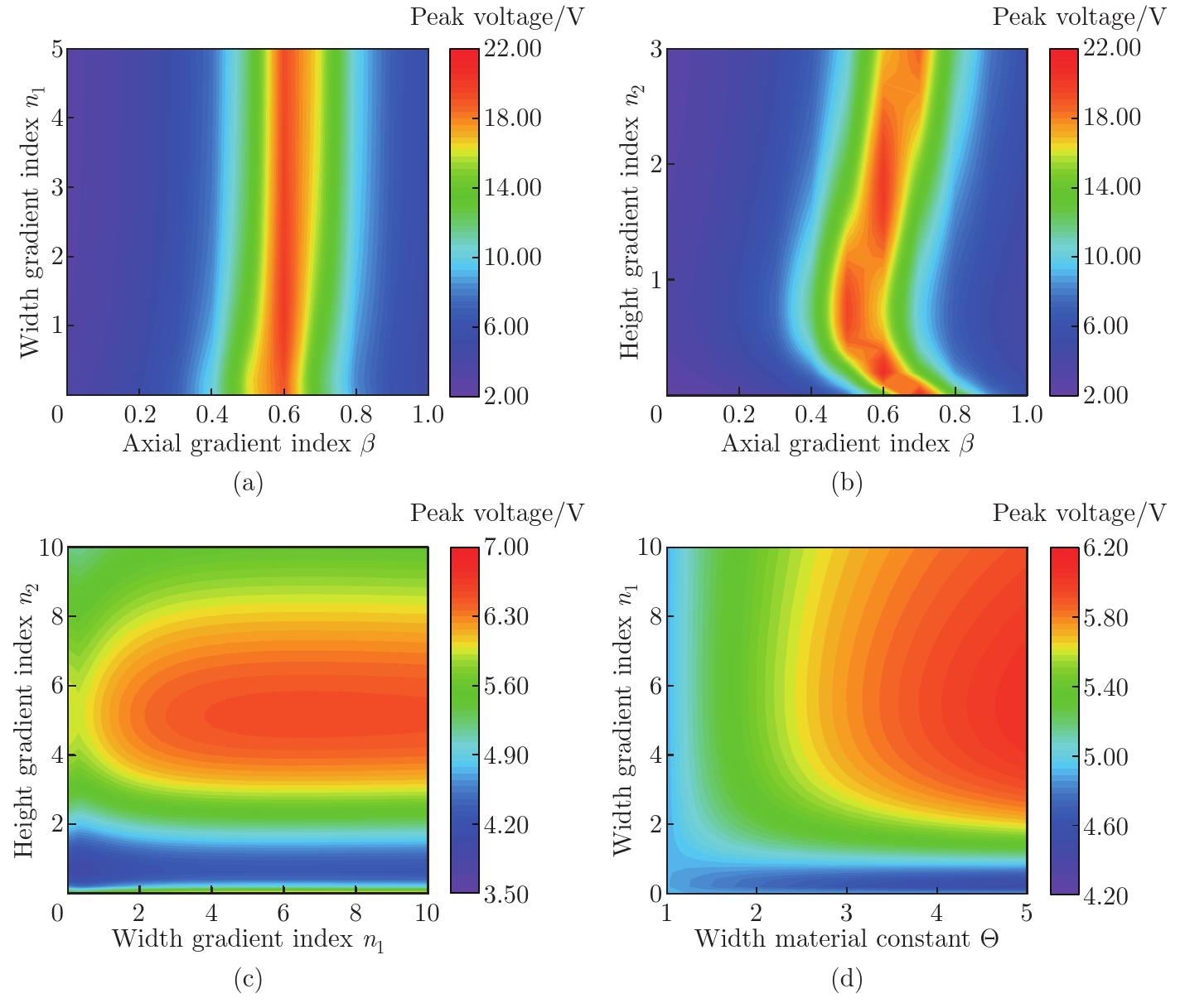
Fig. 6
Output peak voltage of the 3D FG pipe energy harvester at a given excitation frequency of f=53 Hz, under interactive effects of different FGM parameters: (a) the relationship between the axial and width gradient indices; (b) the relationship between the axial and height gradient indices; (c) the relationship between the width and height gradient indices; (d) the relationship between the material constant and width gradient index (color online)"
Fig. 7
Output energy of the 3D FG pipe energy harvester under the effect of the load resistance: (a) the tip amplitude; (b) the output peak voltage; (c) the output peak current; (d) the output peak power (color online)"
Fig. 8
Output peak power of the 3D FG pipe energy harvester as a function of the frequency and load resistance: (a) the mode 1; (b) the mode 2 (color online)"
Fig. 9
Maximum peak voltage in the first mode under interactive effects of the piezoelectric layer thickness and load resistance (color online)"
Fig. 10
Output peak voltage of the 3D FG pipe energy harvester as a function of the frequency and flow velocity: (a) the mode 1; (b) the mode 2 (color online)"
Fig. 11
Maximum peak voltage of the first mode as a function of the flow velocity and flow cross-sectional area (color online)"
| [1] | ROUNDY, S. and WRIGHT, P. K.A piezoelectric vibration based generator for wireless electronics. Smart Materials and Structures, 13, 1131–1142 (2004) |
| [2] | ERTURK, A. and INMAN, D. J.A distributed parameter electromechanical model for cantilevered piezoelectric energy harvesters. Journal of Vibration and Acoustics-Transactions of the ASME, 130, 041002 (2008) |
| [3] | SODANO, H. A., PARK, G., and INMAN, D. J.Estimation of electric charge output for piezoelectric energy harvesting. Strain, 40, 49–58 (2004) |
| [4] | DU TOIT, N. E., WARDLE, B. L., and KIM, S. G.Design considerations for MEMS-scale piezoelectric mechanical vibration energy harvesters. Integrated Ferroelectrics, 71, 121–160 (2005) |
| [5] | ERTURK, A. and INMAN, D. J.On mechanical modeling of cantilevered piezoelectric vibration energy harvesters. Journal of Intelligent Material Systems and Structures, 19, 1311–1325 (2008) |
| [6] | ERTURK, A. and INMAN, D. J.An experimentally validated bimorph cantilever model for piezoelectric energy harvesting from base excitations. Smart Materials and Structures, 18, 025009 (2009) |
| [7] | RAFIQUE, S. and BONELLO, P.Experimental validation of a distributed parameter piezoelectric bimorph cantilever energy harvester. Smart Materials and Structures, 19, 094008 (2010) |
| [8] | CAO, D. X., HU, W. H., GAO, Y. H., and GUO, X. Y.Vibration and energy harvesting performance of a piezoelectric phononic crystal beam. Smart Materials and Structures, 28, 085014 (2019) |
| [9] | WANG, X. G., WANG, L., SHU, H. S., and ZHANG, L.Research on dual-functional characteristics of piezoelectric metamaterial beams for vibration reduction and power generation. AIP Advances, 12, 025326 (2022) |
| [10] | MENG, Y., LU, Z. Q., DING, H., and CHEN, L. Q.Plate theory based modeling and analysis of nonlinear piezoelectric composite circular plate energy harvesters. Nonlinear Dynamics, 112, 5129–5149 (2024) |
| [11] | DENG, T., ZHAO, L. K., and JIN, F.Dual-functional perforated metamaterial plate for amplified energy harvesting of both acoustic and flexural waves. Thin-Walled Structures, 197, 111615 (2024) |
| [12] | DU, W. Q., XIANG, Z. J., and QIU, X. B.A semi-analytical electromechanical model for energy harvesting of plate with acoustic black hole indentations. Thin-Walled Structures, 203, 112235 (2024) |
| [13] | WANG, J. L., ZHANG, C. Y., ZHANG, M. J., ABDELKEFI, A., YU, H. Y., GE, X. M., and LIU, H. D.Enhancing energy harvesting from flow-induced vibrations of a circular cylinder using a downstream rectangular plate: an experimental study. International Journal of Mechanical Sciences, 211, 106781 (2021) |
| [14] | ZHANG, Y. S., WANG, W. S., ZHENG, R. C., NAKANO, K., and CARTMELL, M. P.A piezoelectric cantilever-asymmetric-conical-pendulum-based energy harvesting under multi-directional excitation. Journal of Sound and Vibration, 569, 118080 (2024) |
| [15] | FU, H. L., JIANG, J. J., HU, S. J., RAO, J., and THEODOSSIADES, S.A multi-stable ultra-low frequency energy harvester using a nonlinear pendulum and piezoelectric transduction for self-powered sensing. Mechanical Systems and Signal Processing, 189, 110034 (2023) |
| [16] | UENO, H., TOSHIYOSHI, H., and SUZUKI, T.Frequency conversion interposer with no-internal stress curved-beam for MEMS vibrational energy harvesters. Sensors and Actuators A: Physical, 378, 115750 (2024) |
| [17] | MUSCALU, G., FIRTAT, B., ANGHELESCU, A., MOLDOVAN, C., DINULESCU, S., BRASOVEANU, C., EKWINSKA, M., SZMIGIEL, D., ZABOROWSKI, M., ZAJAC, J., STAN, I., and TULBURE, A.Piezoelectric MEMS energy harvester for low-power applications. Electronics, 13, 2087 (2024) |
| [18] | CHEN, Y. B. and YAN, Z.Nonlinear analysis of axially loaded piezoelectric energy harvesters with flexoelectricity. International Journal of Mechanical Sciences, 173, 105473 (2020) |
| [19] | ZHANG, C. L., CHEN, W. Q., and ZHANG, C.Two-dimensional theory of piezoelectric plates considering surface effect. European Journal of Mechanics-A/Solids, 41, 50–57 (2013) |
| [20] | GUO, Y. C. and DING, H.Theoretical and experimental study on dynamic characteristics of L-shaped fluid-conveying pipes. Applied Mathematical Modelling, 129, 232–249 (2024) |
| [21] | YUAN, J. R. and DING, H.Dynamic model of curved pipe conveying fluid based on the absolute nodal coordinate formulation. International Journal of Mechanical Sciences, 232, 107625 (2022) |
| [22] | ZHOU, J., CHANG, X. P., XIONG, Z. J., and LI, Y. H.Stability and nonlinear vibration analysis of fluid-conveying composite pipes with elastic boundary conditions. Thin-Walled Structures, 179, 109597 (2022) |
| [23] | CAO, R. Q., GUO, Z. L., CHEN, W., DAI, H. L., and WANG, L.Nonlinear dynamics of a circular curved cantilevered pipe conveying pulsating fluid based on the geometrically exact model. Applied Mathematics and Mechanics (English Edition), 45, 261–276 (2024) https://doi.org/10.1007/s10483-024-3084-7 |
| [24] | ZHOU, K., DAI, H. L., WANG, L., NI, Q., and HAGEDORN, P.Modeling and nonlinear dynamics of cantilevered pipe with tapered free end concurrently subjected to axial internal and external flows. Mechanical Systems and Signal Processing, 169, 108794 (2022) |
| [25] | DING, H. and JI, J. C.Vibration control of fluid-conveying pipes: a state-of-the-art review. Applied Mathematics and Mechanics (English Edition), 44, 1423–1456 (2023) https://doi.org/10.1007/s10483-023-3023-9 |
| [26] | LIANG, F. and CHEN, Z. Q.Enhanced dynamical stability of rotating composite pipes conveying fluid by a smart piezoelectric design. Applied Mathematical Modelling, 138, 115798 (2025) |
| [27] | LIANG, F. and CHEN, Z. Q.Electro-mechanical vibration control of functionally graded marine risers by a piezoelectric meta-structure design. Applied Ocean Research, 154, 104388 (2025) |
| [28] | DENG, T. C. and DING, H.Frequency band preservation: pipe design strategy away from resonance. Acta Mechanica Sinica, 40, 523201 (2023) |
| [29] | CHEN, W., YAN, H., CAO, R. Q., DAI, H. L., and WANG, L.Theoretical and experimental investigations on large-deformation dynamics of the standing cantilevered pipe conveying fluid. Mechanical Systems and Signal Processing, 220, 111688 (2024) |
| [30] | LI, M. W., YAN, H., and WANG, L.Data-driven model reduction for pipes conveying fluid via spectral submanifolds. International Journal of Mechanical Sciences, 277, 109414 (2024) |
| [31] | ZHU, B., FENG, J. Z., GUO, Y., and WANG, Y. Q.Exact closed-form solution for buckling and free vibration of pipes conveying fluid with intermediate elastic supports. Journal of Sound and Vibration, 596, 118762 (2025) |
| [32] | CAO, D. X., WANG, J. R., GUO, X. Y., LAI, S. K., and SHEN, Y. J.Recent advancement of flow-induced piezoelectric vibration energy harvesting techniques: principles, structures, and nonlinear designs. Applied Mathematics and Mechanics (English Edition), 43, 959–978 (2022) https://doi.org/10.1007/s10483-022-2867-7 |
| [33] | CHATTERJEE, R., SHAH, C. L., GUPTA, S., and SARKAR, S.Energy harvesting in a flow-induced vibrating flapper with biomimetic gaits. International Journal of Mechanical Sciences, 272, 109150 (2024) |
| [34] | DAI, H. L., ABDELMOULA, H., ABDELKEFI, A., and WANG, L.Towards control of cross-flow-induced vibrations based on energy harvesting. Nonlinear Dynamics, 88, 2329–2346 (2017) |
| [35] | MA, X. Q., CHEN, G. T., LI, Z. Y., LITAK, G., and ZHOU, S. X.Nonlinear dynamic characteristics of the multistable wake-galloping energy harvester. Nonlinear Dynamics, 112, 10937–10958 (2024) |
| [36] | MA, X. Q. and ZHOU, S. X.A review of flow-induced vibration energy harvesters. Energy Conversion and Management, 254, 115223 (2022) |
| [37] | MUTSUDA, H., TANAKA, Y., PATEL, R., and DOI, Y.Harvesting flow-induced vibration using a highly flexible piezoelectric energy device. Applied Ocean Research, 68, 39–52 (2017) |
| [38] | WANG, J. L., GENG, L. F., DING, L., ZHU, H. J., and YURCHENKO, D.The state-of-the-art review on energy harvesting from flow-induced vibrations. Applied Energy, 267, 114902 (2020) |
| [39] | WANG, J. L., GENG, L. F., ZHOU, S. X., ZHANG, Z. E., LAI, Z. H., and YURCHENKO, D.Design, modeling and experiments of broadband tristable galloping piezoelectric energy harvester. Acta Mechanica Sinica, 36, 592–605 (2020) |
| [40] | ZHOU, M. Y., FU, Y., LIU, L., XU, Z. L., AL-FURJAN, M. S. H., and WANG, W.Modeling and preliminary analysis of piezoelectric energy harvester based on cylindrical tube conveying fluctuating fluid. Meccanica, 53, 2379–2392 (2018) |
| [41] | LUMENTUT, M. F. and FRISWELL, M. I.A smart pipe energy harvester excited by fluid flow and base excitation. Acta Mechanica, 229, 4431–4458 (2018) |
| [42] | LUMENTUT, M. F. and FRISWELL, M. I.Powering smart pipes with fluid flow: effect of velocity profiles. Computers & Structures, 258, 106680 (2022) |
| [43] | YANG, T., ZHOU, S. X., FANG, S. T., QIN, W. Y., and INMAN, D. J.Nonlinear vibration energy harvesting and vibration suppression technologies: designs, analysis, and applications. Applied Physics Reviews, 8, 031317 (2021) |
| [44] | LIU, C. C. and JING, X. J.Nonlinear vibration energy harvesting with adjustable stiffness, damping and inertia. Nonlinear Dynamics, 88, 79–95 (2017) |
| [45] | YAO, M. H., WANG, X. F., WU, Q. L., NIU, Y., and WANG, S. H.Dynamic analysis and design of power management circuit of the nonlinear electromagnetic energy harvesting device for the automobile suspension. Mechanical Systems and Signal Processing, 170, 108831 (2022) |
| [46] | WANG, G. and SHEN, J. W.Flutter instabilities of cantilevered piezoelectric pipe conveying fluid. Journal of Intelligent Material Systems and Structures, 30, 606–617 (2019) |
| [47] | LU, Z. Q., CHEN, J., DING, H., and CHEN, L. Q.Energy harvesting of a fluid-conveying piezoelectric pipe. Applied Mathematical Modelling, 107, 165–181 (2022) |
| [48] | ZHU, B., CHEN, X. C., GUO, Y., and LI, Y. H.Static and dynamic characteristics of the post-buckling of fluid-conveying porous functionally graded pipes with geometric imperfections. International Journal of Mechanical Sciences, 189, 105947 (2021) |
| [49] | DING, Y. H., CHEN, Z. Q., LIANG, F., LEE, H. P., YU, H., LIN, S. C., and LUO, J.Flexural vibration control of functionally graded poroelastic pipes via periodic piezoelectric design. Acta Mechanica, 235, 3131–3147 (2024) |
| [50] | CHANG, X. P. and ZHOU, J.Static and dynamic characteristics of post-buckling of porous functionally graded pipes under thermal shock. Composite Structures, 288, 115373 (2022) |
| [51] | MAO, J. J., WANG, Y. J., ZHANG, W., WU, M. Q., LIU, Y. Z., and LIU, X. H.Vibration and wave propagation in functionally graded beams with inclined cracks. Applied Mathematical Modelling, 118, 166–184 (2023) |
| [52] | QIU, N., ZHANG, J. Z., LI, C. Y., SHEN, Y. J., and FANG, J. G.Mechanical properties of three-dimensional functionally graded triply periodic minimum surface structures. International Journal of Mechanical Sciences, 246, 108118 (2023) |
| [53] | TANG, Y., WANG, G., REN, T. L., DING, Q., and YANG, T. Z.Nonlinear mechanics of a slender beam composited by three-directional functionally graded materials. Composite Structures, 270, 114088 (2021) |
| [54] | WANG, J. X., WANG, Y. Q., and CHAI, Q. D.Free vibration analysis of a spinning functionally graded spherical-cylindrical-conical shell with general boundary conditions in a thermal environment. Thin-Walled Structures, 180, 109768 (2022) |
| [55] | ZHENG, Y., ZHANG, W., LIU, T., and ZHANG, Y. F.Resonant responses and double-parameter multi-pulse chaotic vibrations of graphene platelets reinforced functionally graded rotating composite blade. Chaos Solitons & Fractals, 156, 111855 (2022) |
| [56] | LIANG, F., GAO, A., and YANG, X. D.Dynamical analysis of spinning functionally graded pipes conveying fluid with multiple spans. Applied Mathematical Modelling, 83, 454–469 (2020) |
| [57] | CHAI, Q. D. and WANG, Y. Q.Traveling wave vibration of graphene platelet reinforced porous joined conical-cylindrical shells in a spinning motion. Engineering Structures, 252, 113718 (2022) |
| [58] | WANG, Y. Q., YE, C., and ZU, J. W.Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerospace Science and Technology, 85, 359–370 (2019) |
| [59] | BISWAL, A. R., ROY, T., and BEHERA, R. K.Optimal vibration energy harvesting from non-prismatic axially functionally graded piezolaminated cantilever beam using genetic algorithm. Journal of Intelligent Material Systems and Structures, 28, 1957–1976 (2017) |
| [60] | QI, L.Energy harvesting properties of the functionally graded flexoelectric microbeam energy harvesters. Energy, 171, 721–730 (2019) |
| [61] | CAO, Y. J., HUANG, H. W., ZHU, Z. H., and SU, S. K.Optimized energy harvesting through piezoelectric functionally graded cantilever beams. Smart Materials and Structures, 28, 025038 (2019) |
| [62] | LARKIN, K., HUNTER, A., and ABDELKEFI, A.Size-dependent modeling and performance enhancement of functionally graded piezoelectric energy harvesters. Journal of Nanoparticle Research, 22, 225 (2020) |
| [63] | ADHIKARI, J., KUMAR, A., KUMAR, R., and JAIN, S. C.Performance enhancement of functionally graded piezoelectric tile by tailoring poling orientation. Mechanics Based Design of Structures and Machines, 51, 3759–3778 (2023) |
| [64] | MOTLAGH, P. L., ANAMAGH, M. R., BEDIZ, B., and BASDOGAN, I.Electromechanical analysis of functionally graded panels with surface-integrated piezo-patches for optimal energy harvesting. Composite Structures, 263, 113714 (2021) |
| [65] | TANG, Y., WANG, G., YANG, T. Z., and DING, Q.Nonlinear dynamics of three-directional functional graded pipes conveying fluid with the integration of piezoelectric attachment and nonlinear energy sink. Nonlinear Dynamics, 111, 2415–2442 (2023) |
| [66] | ERTURK, A. and INMAN, D. J.Piezoelectric Energy Harvesting, 1st ed, John Wiley & Sons, Ltd., West Sussex (2011) |
| [1] | Jinming FAN, Zhongbiao PU, Jie YANG, Xueping CHANG, Yinghui LI. Orthogonality conditions and analytical response solutions of damped gyroscopic double-beam system: an example of pipe-in-pipe system [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 927-946. |
| [2] | Donghai HAN, Qi JIA, Yuanyu GAO, Qiduo JIN, Xin FANG, Jihong WEN, Dianlong YU. Local resonance metamaterial-based integrated design for suppressing longitudinal and transverse waves in fluid-conveying pipes [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1821-1840. |
| [3] | Yang JIN, Tianzhi YANG. Enhanced vibration suppression and energy harvesting in fluid-conveying pipes [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1487-1496. |
| [4] | Hu DING, J. C. JI. Vibration control of fluid-conveying pipes: a state-of-the-art review [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1423-1456. |
| [5] | Bo DOU, Hu DING, Xiaoye MAO, Sha WEI, Liqun CHEN. Dynamic modeling of fluid-conveying pipes restrained by a retaining clip [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(8): 1225-1240. |
| [6] | Jian ZANG, Ronghuan XIAO, Yewei ZHANG, Liqun CHEN. A novel way for vibration control of FGM fluid-conveying pipes via NiTiNOL-steel wire rope [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(6): 877-896. |
| [7] | Xumin GUO, Chunliang XIAO, Hui MA, Hui LI, Xufang ZHANG, Bangchun WEN. Improved frequency modeling and solution for parallel liquid-filled pipes considering both fluid-structure interaction and structural coupling [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(8): 1269-1288. |
| [8] | Sha WEI, Xiong YAN, Xin FAN, Xiaoye MAO, Hu DING, Liqun CHEN. Vibration of fluid-conveying pipe with nonlinear supports at both ends [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(6): 845-862. |
| [9] | Runqing CAO, Zhijian WANG, Jian ZANG, Yewei ZHANG. Resonance response of fluid-conveying pipe with asymmetric elastic supports coupled to lever-type nonlinear energy sink [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(12): 1873-1886. |
| [10] | Xiangjian DUAN, Dongxing CAO, Xiaoguang LI, Yongjun SHEN. Design and dynamic analysis of integrated architecture for vibration energy harvesting including piezoelectric frame and mechanical amplifier [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(6): 755-770. |
| [11] | E. KHANJANI, A. HAJARIAN, A. KARGAR-ESTAHBANATY, N. ARBABI, A. TAHERI, M. BAGHANI. Design and fluid-structure interaction analysis for a microfluidic T-junction with chemo-responsive hydrogel valves [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(6): 939-952. |
| [12] | Tianli JIANG, Huliang DAI, Kun ZHOU, Lin WANG. Nonplanar post-buckling analysis of simply supported pipes conveying fluid with an axially sliding downstream end [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(1): 15-32. |
| [13] | M. HAJHOSSEINI, M. RAFEEYAN. Modeling and analysis of piezoelectric beam with periodically variable cross-sections for vibration energy harvesting [J]. Applied Mathematics and Mechanics (English Edition), 2016, 37(8): 1053-1066. |
| [14] | Shiliang HU, Chuanjing LU, Yousheng HE. Fluid-structure interaction simulation of three-dimensional flexible hydrofoil in water tunnel [J]. Applied Mathematics and Mechanics (English Edition), 2016, 37(1): 15-26. |
| [15] | A. K. VASHISHTH, A. DAHIYA, V. GUPTA. Generalized Bleustein-Gulyaev type waves in layered porous piezoceramic structure [J]. Applied Mathematics and Mechanics (English Edition), 2015, 36(9): 1223-1242. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||
