Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (5): 927-946.doi: https://doi.org/10.1007/s10483-025-3247-6
Previous Articles Next Articles
Jinming FAN1, Zhongbiao PU1, Jie YANG1, Xueping CHANG2,†( ), Yinghui LI1
), Yinghui LI1
Received:2024-11-27
Revised:2025-03-04
Published:2025-05-07
Contact:
Xueping CHANG, E-mail: xuepingch0952@sina.comSupported by:2010 MSC Number:
Jinming FAN, Zhongbiao PU, Jie YANG, Xueping CHANG, Yinghui LI. Orthogonality conditions and analytical response solutions of damped gyroscopic double-beam system: an example of pipe-in-pipe system. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 927-946.
Table 1
Eigenvalues of the original and adjoint systems of the damped PIP systems with different flow velocities"
| Flow velocity | Mode | ||||
|---|---|---|---|---|---|
| 11.909 9+0.026 6i | 11.909 9+0.026 6i | ||||
| 23.231 6+0.117 0i | 23.231 6+0.117 0i | ||||
| 41.244 2+0.065 3i | 41.244 2+0.065 3i | ||||
| 59.864 0+0.078 8i | 59.864 0+0.078 8i | ||||
| 9.290 6+0.029 6i | 9.290 6+0.029 6i | ||||
| 22.533 7+0.110 5i | 22.533 7+0.110 5i | ||||
| 37.495 5+0.068 7i | 37.495 5+0.068 7i | ||||
| 59.834 8+0.077 0i | 59.834 8+0.077 0i |

Fig. 6
Transient response time history diagrams of the damped PIP system when the system is applied with a harmonic excitation f(ξ, τ)=0.01 cos(20τ)δ(ξ−0.5) (uL=3, ke=200, ce=0.1, ci=0.05, co=0.05): (a) analytical solutions (present method); (b) numerical solutions (MSM); (c), (d), and (e) partially enlarged images (color online)"
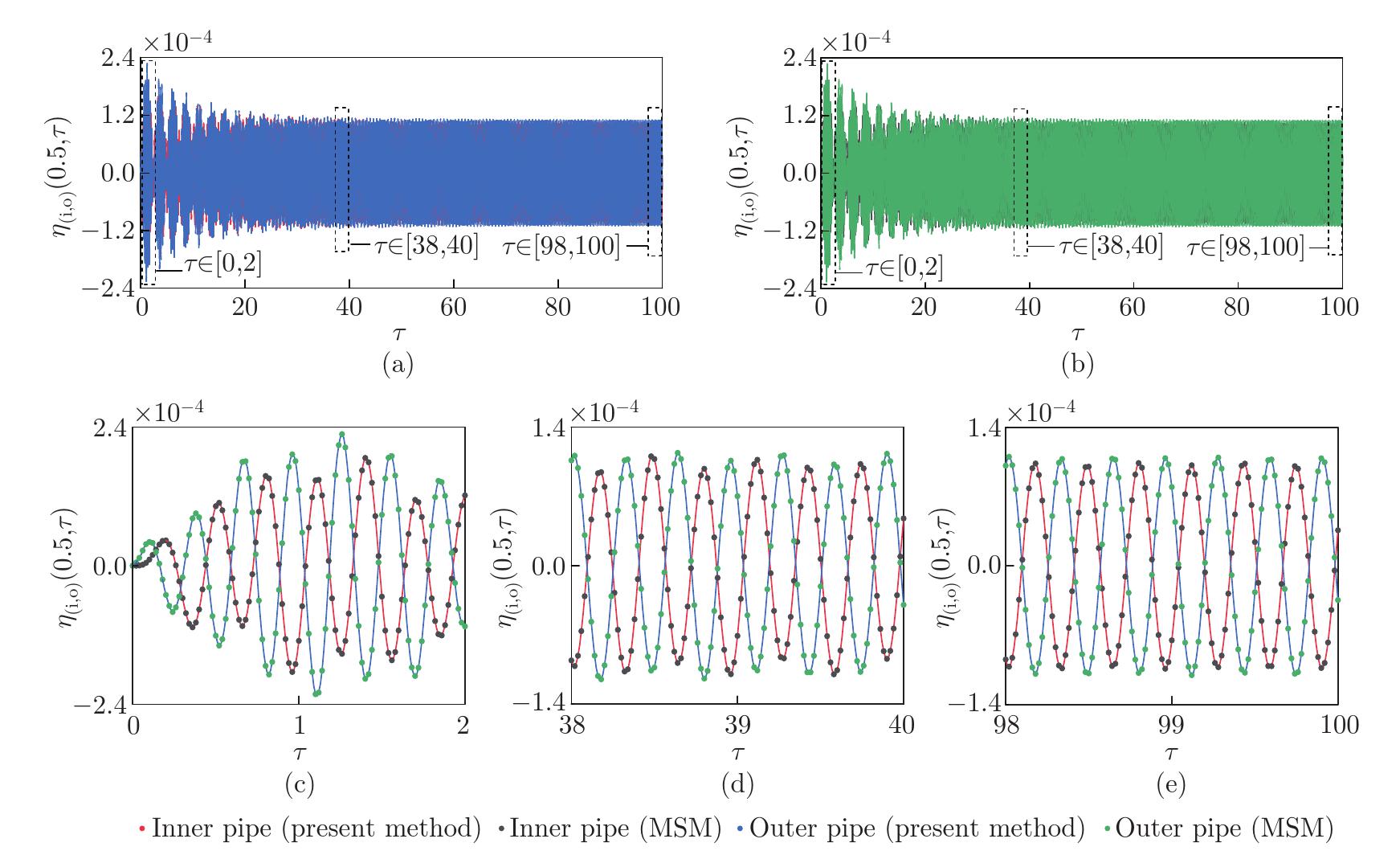
Fig. 8
Transient response time history diagrams of the damped PIP system when the system is applied with a harmonic excitation f(ξ, τ)=0.01 cos(15τ)δ(ξ−0.5) between τ=20 and τ=40 (uL=3, ke=200, ce=0.1, ci=0.05, co=0.05): (a) analytical solutions (present method); (b) numerical solutions (MSM); (c), (d), and (e) partially enlarged images (color online)"

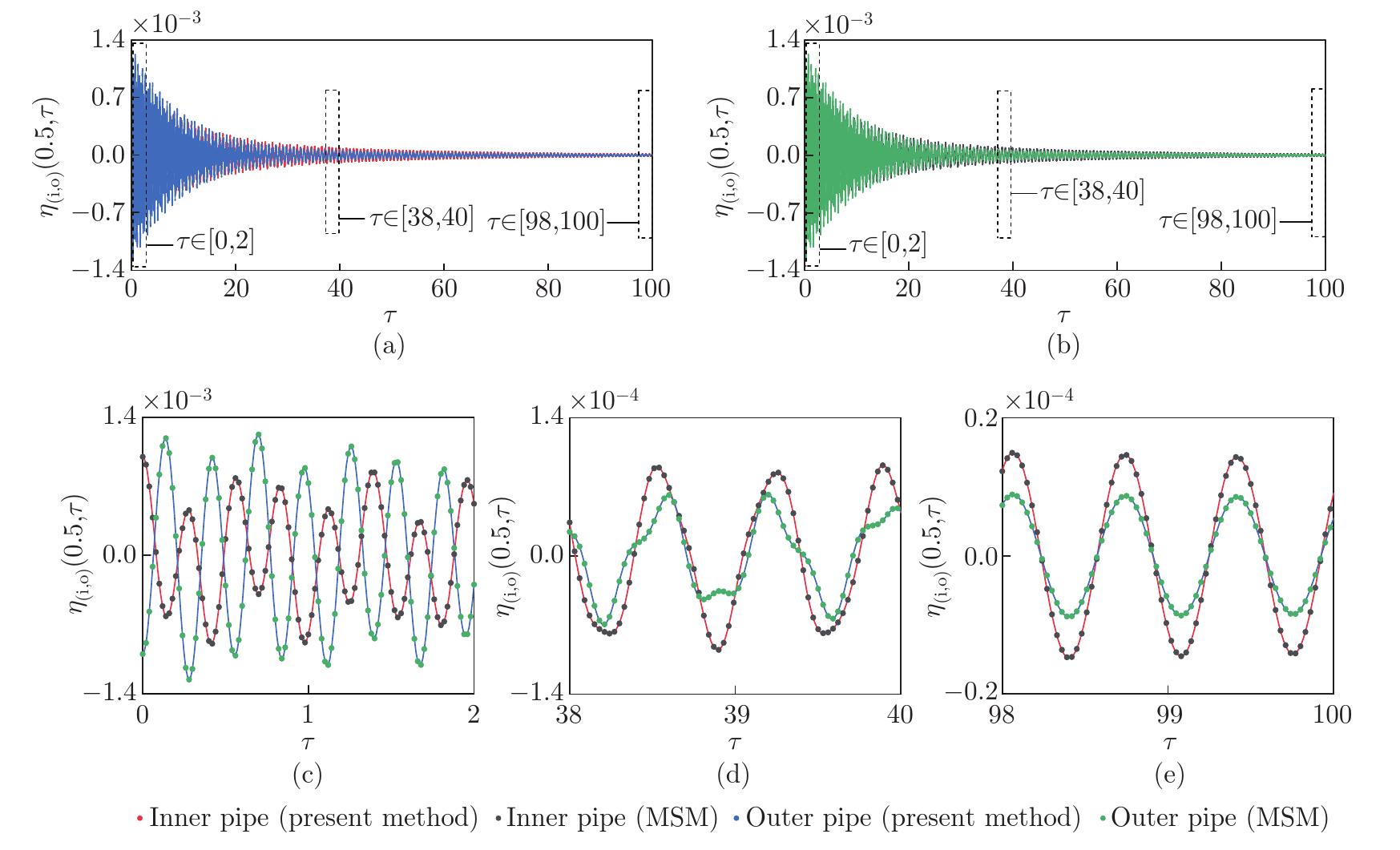
Fig. 9
Transient response time history diagrams of the damped PIP system when the initial conditions of the system are ηi(ξ, 0)=0.001 sin(ξπ) and ηo(ξ, 0)=−0.001 sin(ξπ) (uL=3, ke=200, ce=0.1, ci=0.05, and co=0.05): (a) analytical solutions (present method); (b) numerical solutions (MSM); (c), (d), and (e) are partially enlarged images (color online)"
| [1] | LIU, S. B. and YANG, B. G.A closed-form analytical solution method for vibration analysis of elastically connected double-beam systems. Composite Structures, 212, 598–608 (2019) |
| [2] | HAN, F., DAN, D. H., and DENG, Z. C.A dynamic stiffness-based modal analysis method for a double-beam system with elastic supports. Mechanical Systems and Signal Processing, 146, 106978 (2021) |
| [3] | MATIN-NIKOO, H., BI, K., and HAO, H.Passive vibration control of cylindrical offshore components using pipe-in-pipe (PIP) concept: an analytical study. Ocean Engineering, 142, 39–50 (2017) |
| [4] | KUANG, Y. D., HE, X. Q., CHEN, C. Y., and LI, G. Q.Analysis of nonlinear vibrations of double-walled carbon nanotubes conveying fluid. Computational Materials Science, 45, 875–880 (2009) |
| [5] | VU, H. V., ORDÓÑEZ, A. M., and KARNOPP, B. H.Vibration of a double-beam system. Journal of Sound and Vibration, 229, 807–822 (2000) |
| [6] | LI, Y. X., HU, Z. J., and SUN, L. Z.Dynamical behavior of a double-beam system interconnected by a viscoelastic layer. International Journal of Mechanical Sciences, 105, 291–303 (2016) |
| [7] | LI, Y. X. and SUN, L. Z.Transverse vibration of an undamped elastically connected double-beam system with arbitrary boundary conditions. Journal of Engineering Mechanics, 142, 04015070 (2016) |
| [8] | LI, Y. X., XIONG, F., XIE, L. Z., and SUN, L. Z.State-space approach for transverse vibration of double-beam systems. International Journal of Mechanical Sciences, 189, 105974 (2021) |
| [9] | PALMERI, A. and ADHIKARI, S.A Galerkin-type state-space approach for transverse vibrations of slender double-beam systems with viscoelastic inner layer. Journal of Sound and Vibration, 330, 6372–6386 (2011) |
| [10] | GUO, Y., ZHU, B., ZHAO, X., CHEN, B., and LI, Y. H.Dynamic characteristics and stability of pipe-in-pipe system conveying two-phase flow in thermal environment. Applied Ocean Research, 103, 102333 (2020) |
| [11] | DENG, H., CHEN, K., CHENG, W., and ZHAO, S.Vibration and buckling analysis of double-functionally graded Timoshenko beam system on Winkler-Pasternak elastic foundation. Composite Structures, 160, 152–168 (2017) |
| [12] | ZHAO, X., CHEN, B., LI, Y. H., ZHU, W. D., NKIEGAING, F. J., and SHAO, Y. B.Forced vibration analysis of Timoshenko double-beam system under compressive axial load by means of Green's functions. Journal of Sound and Vibration, 464, 115001 (2020) |
| [13] | CHEN, B., LIN, B. C., ZHAO, X., ZHU, W. D., YANG, Y. K., and LI, Y. H.Closed-form solutions for forced vibrations of a cracked double-beam system interconnected by a viscoelastic layer resting on Winkler-Pasternak elastic foundation. Thin-Walled Structures, 163, 107688 (2021) |
| [14] | CHEN, B., LIN, B. C., LI, Y. H., and TANG, H. P.Exact solutions for steady-state dynamic responses of a laminated composite double-beam system interconnected by a viscoelastic layer in hygrothermal environments. Composite Structures, 268, 113939 (2021) |
| [15] | ONISZCZUK, Z.Forced transverse vibrations of an elastically complex simply supported double-beam system. Journal of Sound and Vibration, 264, 273–286 (2003) |
| [16] | WU, Y. X. and GAO, Y. F.Dynamic response of a simply supported viscously damped double-beam system under a moving oscillator. Journal of Sound and Vibration, 384, 194–209 (2016) |
| [17] | ZHAO, X., MENG, S. Y., ZHU, W. D., ZHU, Y. L., and LI, Y. H.A closed-form solution of forced vibration of a double-curved-beam system by means of the Green's function method. Journal of Sound and Vibration, 561, 117812 (2023) |
| [18] | LI, J. and HUA, H. X.Spectral finite element analysis of elastically connected double-beam systems. Finite Elements in Analysis and Design, 43, 1155–1168 (2007) |
| [19] | ZHAO, X. Z. and CHANG, P.Free and forced vibration of double beam with arbitrary end conditions connected withviscoelastic layer and discrete points. International Journal of Mechanical Sciences, 209, 106707 (2021) |
| [20] | LANGTHJEM, M. A. and SUGIYAMA, Y.Vibration and stability analysis of cantilevered two-pipe systems conveying different fluids. Journal of Fluids and Structures, 13, 251–268 (1999) |
| [21] | ZHANG, Y. F., YAO, M. H., ZHANG, W., and WEN, B. C.Dynamical modeling and multi-pulse chaotic dynamics of a cantilevered pipe conveying pulsating fluid in parametric resonance. Aerospace Science and Technology, 68, 441–453 (2017) |
| [22] | LIANG, F., YANG, X. D., QIAN, Y. J., and ZHANG, W.Transverse free vibration and stability analysis of spinning pipes conveying fluid. International Journal of Mechanical Sciences, 137, 195–204 (2018) |
| [23] | GUO, Y., LI, J. A., ZHU, B., and LI, Y. H.Flow-induced instability and bifurcation in cantilevered composite double-pipe systems. Ocean Engineering, 258, 111825 (2022) |
| [24] | LÜ, L., HU, Y. J., WANG, X. L., LING, L., and LI, C. G.Dynamical bifurcation and synchronization of two nonlinearly coupled fluid-conveying pipes. Nonlinear Dynamics, 79, 2715–2734 (2014) |
| [25] | NI, Q., ZHANG, Z. L., WANG, L., QIAN, Q., and TANG, M.Nonlinear dynamics and synchronization of two coupled pipes conveying pulsating fluid. Acta Mechanica Solida Sinica, 27, 162–171 (2014) |
| [26] | LIU, Z. Y., JIANG, T. L., WANG, L., and DAI, H. L.Nonplanar flow-induced vibrations of a cantilevered PIP structure system concurrently subjected to internal and cross flows. Acta Mechanica Sinica, 35, 1241–1256 (2019) |
| [27] | CHANG, X. P., FAN, J. M., HAN, D. Z., CHEN, B., and LI, Y. H.Stability and modal conversion phenomenon of pipe-in-pipe structures with arbitrary boundary conditions by means of Green's functions. International Journal of Structural Stability and Dynamics, 22, 2250034 (2022) |
| [28] | CHANG, X. P., FAN, J. M., QU, C. J., and LI, Y. H.Coupling vibration of a composite pipe-in-pipe structure subjected to gas-liquid mixed transport by means of Green's functions. Mechanics of Advanced Materials and Structures, 30, 1604–1623 (2022) |
| [29] | CHUNG, C. H. and KAO, I. I.Modeling of axially moving wire with damping: eigenfunctions, orthogonality, and applications in slurry wiresaws. Journal of Sound and Vibration, 330, 2947–2963 (2011) |
| [30] | ZHANG, H. J., MA, J., DING, H., and CHEN, L. Q.Vibration of axially moving beam supported by viscoelastic foundation. Applied Mathematics and Mechanics (English Edition), 38(2), 161–172 (2017) https://doi.org/10.1007/s10483-017-2170-9 |
| [1] | Yueting ZHOU, Qinghui LUO, Lihua WANG, Shenghu DING. Competition between electro-magnetic enhancing and shear stress weakening effects on adhesion behaviors of multiferroic composites [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 831-848. |
| [2] | Tianchi YU, Feng LIANG, Hualin YANG. Vibration energy harvesting of a three-directional functionally graded pipe conveying fluids [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 795-812. |
| [3] | Jufang JIA, Huilin YIN, Qinyu YU, Jiabin SUN, Xinsheng XU, Zhenhuan ZHOU. New analytical solutions for free vibration of embedded magneto-electro-elastic cylindrical shells with step-wise thickness variations [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(3): 447-466. |
| [4] | M. NAVEED, M. IMRAN, T. ASGHAR, Z. ABBAS. Transport mechanism in chemically reactive hybrid nanofluidflow containing gyrotactic micro-organisms overa curved oscillatory surface [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(1): 177-192. |
| [5] | L.I. KUZMINA, Y.V. OSIPOV, A.R. PESTEREV. Deep bed filtration model for cake filtration and erosion [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 355-372. |
| [6] | Xiaodong GUO, Zhu SU, Lifeng WANG. Dynamic characteristics of multi-span spinning beams with elastic constraints under an axial compressive force [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 295-310. |
| [7] | Donghai HAN, Qi JIA, Yuanyu GAO, Qiduo JIN, Xin FANG, Jihong WEN, Dianlong YU. Local resonance metamaterial-based integrated design for suppressing longitudinal and transverse waves in fluid-conveying pipes [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1821-1840. |
| [8] | Jiawei MAO, Hao GAO, Junzhe ZHU, Penglin GAO, Yegao QU. Analytical modeling of piezoelectric meta-beams with unidirectional circuit for broadband vibration attenuation [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1665-1684. |
| [9] | Yang JIN, Tianzhi YANG. Enhanced vibration suppression and energy harvesting in fluid-conveying pipes [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1487-1496. |
| [10] | Hu DING, J. C. JI. Vibration control of fluid-conveying pipes: a state-of-the-art review [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1423-1456. |
| [11] | Bo DOU, Hu DING, Xiaoye MAO, Sha WEI, Liqun CHEN. Dynamic modeling of fluid-conveying pipes restrained by a retaining clip [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(8): 1225-1240. |
| [12] | Jian ZANG, Ronghuan XIAO, Yewei ZHANG, Liqun CHEN. A novel way for vibration control of FGM fluid-conveying pipes via NiTiNOL-steel wire rope [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(6): 877-896. |
| [13] | A. BAKHTIYARI, M. BAGHANI, S. SOHRABPOUR. An investigation on multilayer shape memory polymers under finite bending through nonlinear thermo-visco-hyperelasticity [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(1): 73-88. |
| [14] | Sha WEI, Xiong YAN, Xin FAN, Xiaoye MAO, Hu DING, Liqun CHEN. Vibration of fluid-conveying pipe with nonlinear supports at both ends [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(6): 845-862. |
| [15] | Xiang MU, Xiaoyu FU, Liangliang ZHANG, Zhaowei ZHU, Jinming ZHANG, Yang GAO. Fundamental solutions of critical wedge angles for one-dimensional piezoelectric quasicrystal wedge [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(5): 709-728. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS