Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (2): 209-232.doi: https://doi.org/10.1007/s10483-025-3211-6
Xuefeng WANG1, Zhan SHI2, Qiqi YANG3, Yuzhi CHEN3, Xueyong WEI3, Ronghua HUAN2,†( )
)
Received:2024-09-04
Revised:2024-11-11
Online:2025-02-03
Published:2025-02-02
Contact:
Ronghua HUAN, E-mail: rhhuan@zju.edu.cnSupported by:2010 MSC Number:
Xuefeng WANG, Zhan SHI, Qiqi YANG, Yuzhi CHEN, Xueyong WEI, Ronghua HUAN. Recent advancements of nonlinear dynamics in mode coupled microresonators: a review. Applied Mathematics and Mechanics (English Edition), 2025, 46(2): 209-232.
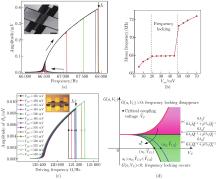
Fig. 1
Frequency locking caused by 1:3 internal resonance: (a) frequency locking in the first-order bending primary mode, in which the inset shows the microscopic image of the micro-resonator[18]; (b) the range of frequency locking[18]; (c) frequency locking in the nonlinear micro-resonator, where the inset shows the microscopic image of the electrostatically coupled micro-resonators[23]; (d) conditions for frequency locking[24] (color online)"
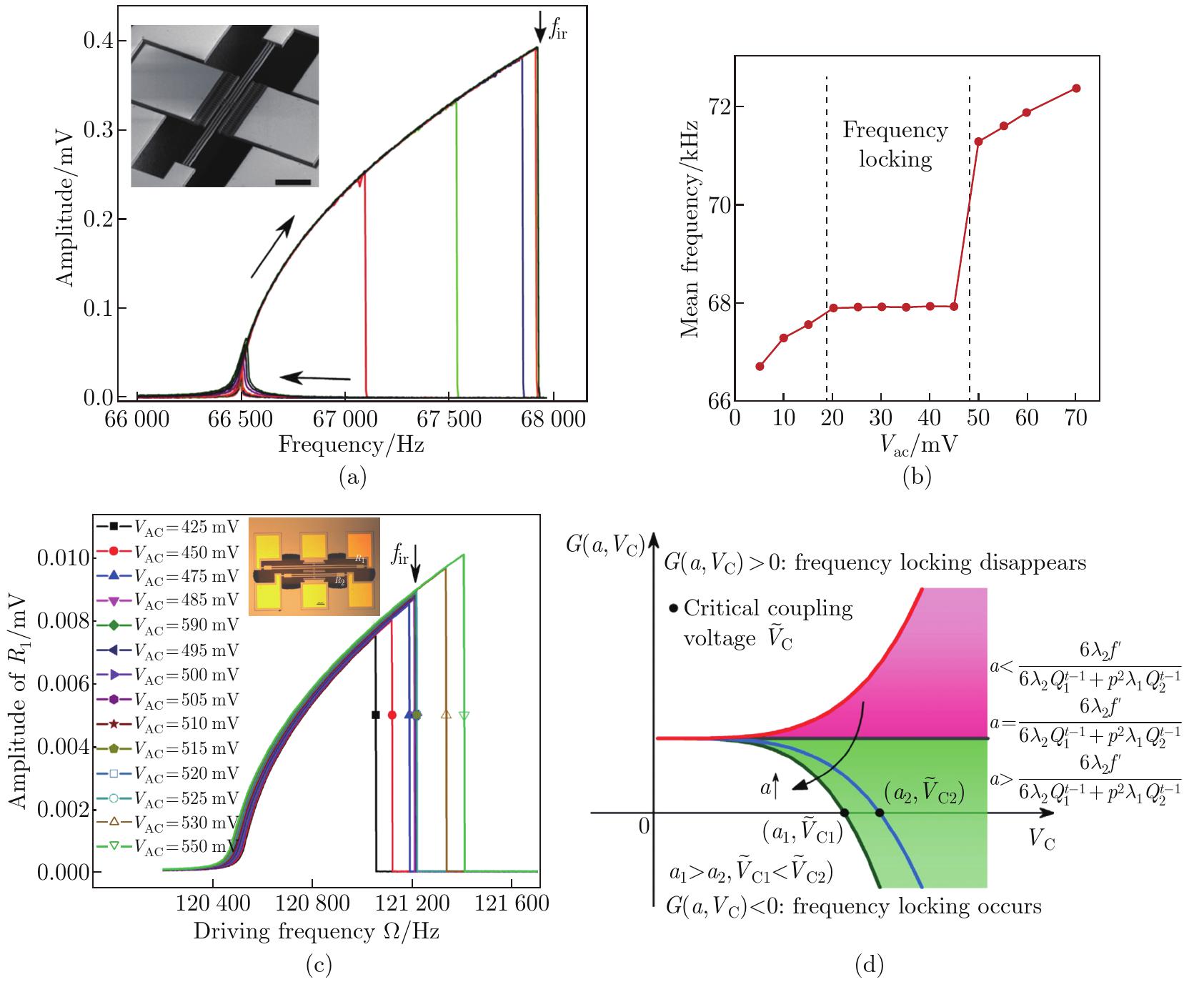
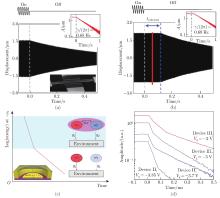
Fig. 2
(a) Displacement response of the low-order primary mode without internal resonance[31]. (b) Displacement response of the low-order primary mode with internal resonance[31]. (c) The mechanism of energy dissipation during internal resonance[32]. (d) The experimental results of energy dissipation[32] (color online)"
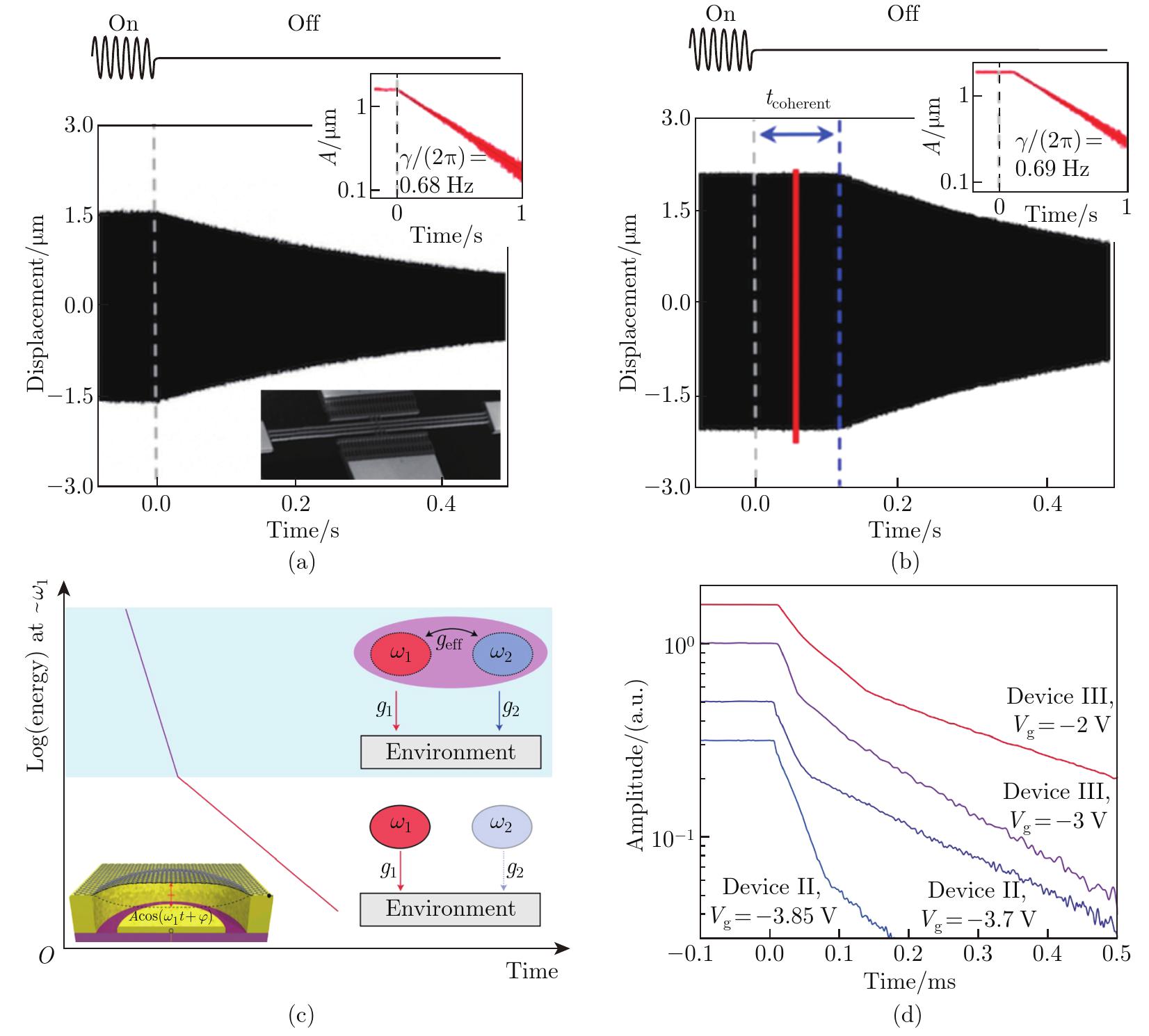
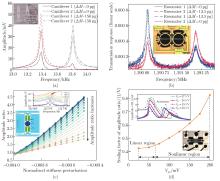
Fig. 6
Mode localization in MEMS resonators: (a) mode localization in mechanically coupled resonators[122]; (b) mode localization in electrostatically coupled resonators[118]; (c) mode localization with harden spring nonlinearity[133]; (d) mode localization with soften spring nonlinearity[134] (color online)"
| [1] | LIFSHITZ, R. and CROSS, M. C. Nonlinear dynamics of nanomechanical and micromechanical resonators. Reviews of Ronlinear Dynamics and Complexity, Wiley, New York (2008) |
| [2] | HAJJAJ, A. Z., JABER, N., ILYAS, S., ALFOSAIL, F. K., and YOUNIS, M. I. Linear and nonlinear dynamics of micro and nano-resonators: review of recent advances. International Journal of Non-Linear Mechanics, 119, 103328 (2020) |
| [3] | STIWARI, S. and CANDLER, R. N. Using flexural mems to study and exploit nonlinearities: a review. Journal of Micromechanics and Microengineering, 29, 083002 (2019) |
| [4] | ZHAO, Z. A., LI, N., QU, Y. L., and CHEN, W. Q. Novel mode-coupling vibrations of AlN thin film bulk acoustic resonator operating with thickness-extensional mode. Applied Mathematics and Mechanics (English Edition), 44(12), 2187–2206 (2023) https://doi.org/10.1007/s10483-023-3056-6 |
| [5] | DING, Z. Y., QIAO, K., ERNST, N., KONG, J., CHEN, M. D., MATTHEWS, L. S., and HYDE, T. W. Nonlinear mode coupling and internal resonance observed in a dusty plasma. New Journal of Physics, 21, 103051 (2019) |
| [6] | ROBERTSON, P., HORNER, J., WITTENMYER, R. A., ENDL, M., COCHRAN, M. D., MACQUEEN, P. J., BRUGAMYER, E. J., SIMON, A. K., BARNES, S. I., and CALDWELL, C. A second giant planet in 3:2 mean-motion resonance in the HD 20431 system. The Astrophysical Journal, 754, 50 (2012) |
| [7] | GORELIK, G. and WITT, A. Swing of an elastic pendulum as an example of two parametrically bound linear vibration systems. Journal of Technical Physics (USSR), 3, 294–307 (1933) |
| [8] | NAYFEH, A. H. and MOOK, D. T. Nonlinear Oscillations, John Wiley & Sons, New York (2008) |
| [9] | NIKPOURIAN, A., GHAZAVI, M. R., and AZIZI, S. Size-dependent modal interactions of a piezoelectrically laminated microarch resonator with 3:1 internal resonance. Applied Mathematics and Mechanics (English Edition), 41 (10), 1517–1538 (2020) https://doi.org/10.1007/s10483-020-2658-6 |
| [10] | ASADI, K., YU, J., and CHO, H. N. Nonlinear couplings and energy transfers in micro- and nano-mechanical resonators: intermodal coupling, internal resonance and synchronization. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 376, 20170141 (2018) |
| [11] | KESKEKLER, A., SHOSHANI, O., LEE, M., VAN DER ZANT, H. S. J., STEENEKEN, P. G., and ALIJANI, F. Tuning nonlinear damping in graphene nanoresonators by parametric-direct internal resonance. Nature Communications, 12, 1099 (2021) |
| [12] | YOUNIS, M. I. and NAYFEH, A. H. A study of the nonlinear response of a resonant microbeam to an electric actuation. Nonlinear Dynamics, 31, 91–117 (2003) |
| [13] | LI, L., ZHANG, Q. C., WANG, W., and HAN, J. X. Nonlinear coupled vibration of electrostatically actuated clamped-clamped microbeams under higher-order modes excitation. Nonlinear Dynamics, 90, 1593–1606 (2017) |
| [14] | VYAS, A., PEROULIS, D., and BAJAJ, A. K. A microresonator design based on nonlinear 1:2 internal resonance in flexural structural modes. Journal of Microelectromechanical Systems, 18, 744–762 (2009) |
| [15] | TRIPATHI, A. and BAJAJ, A. K. Topology optimization and internal resonances in transverse vibrations of hyperelastic plates. International Journal of Solids and Structures, 81, 311–328 (2016) |
| [16] | OUAKAD, H. M. and YOUNIS, M. I. The dynamic behavior of MEMS arch resonators actuated electrically. International Journal of Non-Linear Mechanics, 45, 704–713 (2010) |
| [17] | GUTSCHMIDT, S. and GOTTLIEB, O. Internal resonances and bifurcations of an array below the first pull-in instability. International Journal of Bifurcation and Chaos, 20, 605–618 (2010) |
| [18] | ANTONIO, D., ZANETTE, D. H., and LÓPEZ, D. Frequency stabilization in nonlinear micromechanical oscillators. Nature Communications, 3, 806 (2012) |
| [19] | CZAPLEWSKI, D. A., STRACHAN, S., SHOSHANI, O., SHAW, S. W., and LOPEZ, D. Bifurcation diagram and dynamic response of a mems resonator with a 1:3 internal resonance. Applied Physics Letters, 114, 254104 (2019) |
| [20] | MANGUSSI, F. and ZANETTE, D. H. Internal resonance in a vibrating beam: a zoo of nonlinear resonance peaks. PLoS ONE, 11, e0162365 (2016) |
| [21] | ZANETTE, D. H. Stability of two-mode internal resonance in a nonlinear oscillator. European Physical Journal B, 91, 89 (2018) |
| [22] | ZANETTE, D. H. Effects of noise on the internal resonance of a nonlinear oscillator. Scientific Reports, 8, 5976 (2018) |
| [23] | WANG, X. F., HUAN, R. H., ZHU, W. Q., PU, D., and WEI, X. F. Frequency locking in the internal resonance of two electrostatically coupled micro-resonators with frequency ratio 1:3. Mechanical Systems and Signal Processing, 146, 106981 (2021) |
| [24] | WANG, X. F., HUAN, R. H., ZHU, W. Q., SHI, Z., WEI, X. Y., and CAI, G. Q. Amplitude region for triggering frequency locking in internal resonance response of two nonlinearly coupled micro-resonators. International Journal of Non-Linear Mechanics, 130, 103673 (2021) |
| [25] | LI, L., YANG, W., TIAN, X. G., SHAO, S. J., and ZHANG, W. M. Multimechanical frequency locking mechanism and robustness analysis of MDOF coupled resonator. International Journal of Mechanical Sciences, 276, 109376 (2024) |
| [26] | WEI, X. Y., ZHANG, T. N., JIANG, Z. D., REN, J., and HUAN, R. H. Frequency latching in nonlinear micromechanical resonators. Applied Physics Letters, 110, 143506 (2017) |
| [27] | KIRKENDALL, C. R., HOWARD, D. J., and KWON, J. W. Internal resonance in quartz crystal resonator and mass detection in nonlinear regime. Applied Physics Letters, 103, 223502 (2013) |
| [28] | LIPIÄINEN, L., JAAKKOLA, A., KOKKONEN, K., and KAIVOLA, M. Nonlinear excitation of a rotational mode in a piezoelectrically excited square-extensional mode resonator. Applied Physics Letters, 100, 153508 (2012) |
| [29] | ZHANG, T. N., GUO, C. W., JIANG, Z. D., and WEI, X. Y. Internal resonance between the extensional and flexural modes in micromechanical resonators. Journal of Applied Physics, 126, 164506 (2019) |
| [30] | SHI, Z., PU, D., HUAN, R. H., WANG, X. F., JIANG, Z. D., and WEI, X. Y. Mode interaction induced response flattening in two mechanically coupled micro-resonators. Mechanical Systems and Signal Processing, 177, 109164 (2022) |
| [31] | CHEN, C. Y., ZANETTE, D. H., CZAPLEWSKI, D. A., SHAW, S., and LOPEZ, D. Direct observation of coherent energy transfer in nonlinear micromechanical oscillators. Nature Communications, 8, 15523 (2017) |
| [32] | GÜTTINGER, J., NOURY, A., WEBER, P., ERIKSSON, A. M., LAGOIN, C., MOSER, J., EICHLER, C., WALLRAFF, A., ISACSSON, A., and BACHTOLD, A. Energy-dependent path of dissipation in nanomechanical resonators. Nature Nanotechnology, 12, 631–636 (2017) |
| [33] | HAJJAJ, A. Z., ALFOSAIL, F. K., JABER, N., ILYAS, S., and YOUNIS, M. I. Theoretical and experimental investigations of the crossover phenomenon in micromachined arch resonator: part ii — simultaneous 1:1 and 2:1 internal resonances. Nonlinear Dynamics, 99, 407–432 (2020) |
| [34] | ROCHA, R. T. and YOUNIS, M. I. Nonlinear mode saturation in a U-shaped micro-resonator. Scientific Reports, 12, 10420 (2022) |
| [35] | ALCHEIKH, N., OUAKAD, H. M., BEN-MBAREK, S., and YOUNIS, M. I. Static and dynamic actuations of clamped-clamped V-shaped micro-resonators under electrostatic forces. Mechanical Systems and Signal Processing, 155, 107571 (2021) |
| [36] | SARRAFAN, A., BAHREYNI, B., and GOLNARAGHI, F. Development and characterization of an H-shaped microresonator exhibiting 2:1 internal resonance. Journal of Microelectromechanical Systems, 26, 993–1001 (2017) |
| [37] | KIRKENDALL, C. R. and KWON, J. W. Multistable internal resonance in electroelastic crystals with nonlinearly coupled modes. Scientific Reports, 6, 22897 (2016) |
| [38] | HAJJAJ, A. Z., ABDULLAH-HAFIZ, M. D., and YOUNIS, M. I. Mode coupling and nonlinear resonances of MEMS arch resonators for bandpass filters. Scientific Reports, 7, 41820 (2017) |
| [39] | ZHANG, T. N., WEI, X. Y., JIANG, Z. D., and CUI, T. H. Sensitivity enhancement of a resonant mass sensor based on internal resonance. Applied Physics Letters, 113, 223505 (2018) |
| [40] | SARRAFAN, A., AZIMI, S., GOLNARAGHI, F., and BAHREYNI, B. A nonlinear rate microsensor utilising internal resonance. Scientific Reports, 9, 8648 (2019) |
| [41] | POTEKIN, R., DHARMASENA, S., MCFARLAND, D. M., BERGMAN, L. A., VAKAKIS, A. F., and CHO, H. Cantilever dynamics in higher-harmonic atomic force microscopy for enhanced material characterization. International Journal of Solids and Structures, 110, 332–339 (2017) |
| [42] | YAN, J., BLOOM, M., BAE, S. C., LUIJTEN, E., and GRANICK, S. Linking synchronization to self-assembly using magnetic Janus colloids. nature, 491, 578–581 (2012) |
| [43] | SHAHAL, S., WURZBERG, A., SIBONY, I., DUADI, H., SHNIDERMAN, E., WEYMOUTH, D., DAVIDSON, N., and FRIDMAN, M. Synchronization of complex human networks. Nature Communications, 11, 3854 (2020) |
| [44] | PRINDLE, A., SAMAYOA, P., RAZINKOV, I., DANINO, T., TSIMRING, L. S., and HASTY, J. A sensing array of radically coupled genetic ‘biopixels’. nature, 481, 39–44 (2012) |
| [45] | HUYGENS, C. Horologium Oscillatorium, Dawsons Pall Mall, London (1966) |
| [46] | OSIPOV, G. V., KURTHS, J., and ZHOU, C. S. Synchronization in Oscillatory Networks, Springer Science & Business Media, New York (2007) |
| [47] | JIN, Y. B., LIU, X. W., SHAO, Y. C., WANG, H. T., and YANG, W. High-speed quadrupedal locomotion by imitation-relaxation reinforcement learning. Nature Machine Intelligence, 4, 1198–1208 (2022) |
| [48] | BERGERON, H., SINCLAIR, L. C., SWANN, W. C., KHADER, I., COSSEL, K. C., CERMAK, M., DESCHENES, J. D., and NEWBURY, N. R. Femtosecond time synchronization of optical clocks off of a flying quadcopter. Nature Communications, 10, 1819 (2019) |
| [49] | XU, L., WANG, S. D., JIANG, Z. D., and WEI, X. Y. Programmable synchronization enhanced mems resonant accelerometer. Microsystems & Nanoengineering, 6, 63 (2020) |
| [50] | WEI, X. Y., XU, M. K., YANG, Q. Q., XU, L., QI, Y. H., REN, Z. M., REN, J., HUAN, R. H., and JIANG, Z. D. MEMS huygens clock based on synchronized micromechanical resonators. Engineering, 36, 124–131 (2024) |
| [51] | ZALALUTDINOV, M., AUBIN, K. L., PANDEY, M., ZEHNDER, A. T., RAND, R. H., CRAIGHEAD, H. G., PARPIA, J. M., and HOUSTON, B. H. Frequency entrainment for micromechanical oscillator. Applied Physics Letters, 83, 3281–3283 (2003) |
| [52] | SHIM, S. B., IMBODEN, M., and MOHANTY, P. Synchronized oscillation in coupled nanomechanical oscillators. Science, 316, 95–99 (2007) |
| [53] | AGRAWAL, D. K., WOODHOUSE, J., and SESHIA, A. A. Observation of locked phase dynamics and enhanced frequency stability in synchronized micromechanical oscillators. Physical Review Letters, 111, 084101 (2013) |
| [54] | MATHENY, M. H., GRAU, M., VILLANUEVA, L. G., KARABALIN, R. B., CROSS, M. C., and ROUKES, M. L. Phase synchronization of two anharmonic nanomechanical oscillators. Physical Review Letters, 112, 014101 (2014) |
| [55] | SHOSHANI, O., HEYWOOD, D., YANG, Y. S., KENNY, T. W., and SHAW, S. W. Phase noise reduction in an MEMS oscillator using a nonlinearly enhanced synchronization domain. Journal of Microelectromechanical Systems, 25, 870–876 (2016) |
| [56] | SHOSHANI, O. and SHAW, S. W. Phase noise reduction and optimal operating conditions for a pair of synchronized oscillators. IEEE Transactions on Circuits and Systems I: Regular Papers, 63, 1–11 (2015) |
| [57] | ANTONIO, D., CZAPLEWSKI, D. A., GUEST, J. R., LOPEZ, D., ARROYO, S. I., and ZANETTE, D. H. Nonlinearity-induced synchronization enhancement in micromechanical oscillators. Physical Review Letters, 114, 034103 (2015) |
| [58] | CZAPLEWSKI, D. A., ANTONIO, D., GUEST, J. R., LOPEZ, D., ARROYO, S. I., and ZANETTE, D. H. Enhanced synchronization range from non-linear micromechanical oscillators. 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), IEEE, Anchorage (2015) |
| [59] | TAHERI-TEHRANI, P., DEFOORT, M., and HORSLEY, D. A. Synchronization of a micromechanical oscillator in different regimes of electromechanical nonlinearity. Applied Physics Letters, 111, 183503 (2017) |
| [60] | SHI, Z., PU, D., LV, Q. F., HUAN, R. H., WANG, X. F., XIAO, Z. H., JIANG, Z. D., and WEI, X. Y. Enhancement of synchronization bandwidth in an arch beam. Journal of Sound and Vibration, 545, 117415 (2023) |
| [61] | DEFOORT, M., HENTZ, S., SHAW, S. W., and SHOSHANI, O. Amplitude stabilization in a synchronized nonlinear nanomechanical oscillator. Communications Physics, 5, 93 (2022) |
| [62] | SHI, Z., PU, D., WANG, X. F., HUAN, R. H., JIANG, Z. D., and WEI, X. Y. Phase-delay induced variation of synchronization bandwidth and frequency stability in a micromechanical oscillator. Nonlinear Dynamics, 105, 2981–2994 (2021) |
| [63] | HUAN, R. H., PU, D., WANG, X. F., and WEI, X. Y. Effects of phase delay on synchronization in a nonlinear micromechanical oscillator. Applied Physics Letters, 114, 233501 (2019) |
| [64] | SHI, Z., PU, D., WANG, X. F., WEI, X. Y., and HUAN, R. H. Synchronization process expediting in nonlinear oscillators via reconfiguration of the potential well pattern. International Journal of Mechanical Sciences, 260, 108642 (2023) |
| [65] | YANG, Q. Q., WANG, X. F., DAI, H. S., SHI, Z., SONG, J. H., XU, Y. T., WAN, H. B., HUAN, R. H., and WEI, X. Y. Phase evolution and control in a synchronized duffing-type nonlinear micro-oscillator. Mechanical Systems and Signal Processing, 219, 111598 (2024) |
| [66] | PU, D., WEI, X. Y., XU, L., JIANG, Z. D., and HUAN, R. H. Synchronization of electrically coupled micromechanical oscillators with a frequency ratio of 3:1. Applied Physics Letters, 112, 013503 (2018) |
| [67] | TAHERI-TEHRANI, P., GUERRIERI, A., DEFOORT, M., FRANGI, A., and HORSLEY, D. A. Mutual 3:1 subharmonic synchronization in a micromachined silicon disk resonator. Applied Physics Letters, 111, 183505 (2017) |
| [68] | WEI, X. Y., XU, L., JIANG, Z. D., and HUAN, R. H. MEMS based ultrahigh order frequency multiplication utilizing superharmonic synchronization effect. Sensors and Actuators A-Physical, 332, 113152 (2021) |
| [69] | WANG, D. F., DU, X., WANG, X., IKEHARA, T., and MAEDA, R. Multiplication in frequencies by synchronized and superharmonic oscillations: sensing verification with picogram order microspheres. IEEE Sensors Journal, 15, 4464–4471 (2015) |
| [70] | NAKAJIMA, M., WANG, D. F., IKEHARA, T., ITOH, T., and MAEDA, R. Synchronized oscillation in micro-mechanically coupled oscillator system: part ii — non-synchronized super harmonic oscillation. Symposium on Design, Test, Integration and Packaging of MEMS/MOEMS (DTIP), Barcelona (2013) |
| [71] | XU, L., WANG, S. D., JIANG, Z. D., and WEI, X. Y. Programmable synchronization enhanced MEMS resonant accelerometer. Microsystems & Nanoengineering, 6, 63 (2020) |
| [72] | XU, L., QI, Y. H., JIANG, Z. D., and WEI, X. Y. Fast frequency relocking for synchronization enhanced resonant accelerometer. Microsystems & Nanoengineering, 8, 93 (2022) |
| [73] | ZHANG, H. C., XU, L., DING, Y. Y., JIANG, Z. D., and WEI, X. Y. Capacitance detection based on high order synchronization sensing. IEEE Sensors Journal, 21, 16780–16789 (2021) |
| [74] | PU, D., WEI, X. Y., ZHU, W. X., CHEN, K., JIANG, Z. D., and HUAN, R. H. Amplifying charge-sensing in micromechanical oscillators based on synchronization. Sensors and Actuators A-Physical, 339, 113517 (2022) |
| [75] | MATHENY, M. H., EMENHEISER, J., FON, W., CHAPMAN, A., SALOVA, A., ROHDEN, M., LI, J., DE BADYN, M. H., POSFAI, M., DUENAS-OSORIO, L., MESBAHI, M., CRUTCHFIELD, J. P., CROSS, M. C., D’SOUZA, R. M., and ROUKES, M. L. Exotic states in a simple network of nanoelectromechanical oscillators. Science, 363, eaav7932 (2019) |
| [76] | LI, J., ZHOU, Z. H., WAN, S., ZHANG, Y. L., SHEN, Z., LI, M., ZOU, C. L., GUO, G. C., and DONG, C. H. All-optical synchronization of remote optomechanical systems. Physical Review Letters, 129, 063605 (2022) |
| [77] | COLOMBANO, M. F., ARREGUI, G., CAPUJ, N. E., PITANTI, A., MAIRE, J., GRIOL, A., GARRIDO, B., MARTINEZ, A., SOTOMAYOR-TORRES, C. M., and NAVARRO-URRIOS, D. Synchronization of optomechanical nanobeams by mechanical interaction. Physical Review Letters, 123, 017402 (2019) |
| [78] | LI, J., ZHOU, Z. H., WAN, S., ZHANG, Y. L., SHEN, Z., LI, M., ZOU, C. L., GUO, G. C., and DONG, G. H. All-optical synchronization of remote optomechanical systems. Physical Review Letters, 129, 063605 (2022) |
| [79] | WEISS, T., KRONWALD, A., and MARQUARDT, F. Noise-induced transitions in optomechanical synchronization. New Journal of Physics, 18, 013043 (2016) |
| [80] | HALL, J. L. Nobel lecture: defining and measuring optical frequencies. Reviews of Modern Physics, 78, 1279–1295 (2006) |
| [81] | NEWBURY, N. R. Searching for applications with a fine-tooth comb. Nature Photonics, 5, 186–188 (2011) |
| [82] | PAPP, S. B., BEHA, K., DEL’HAYE, P., QUINLAN, F., LEE, H., VAHALA, K. J., and DIDDAMS, S. A. Microresonator frequency comb optical clock. Optica, 1, 10–14 (2014) |
| [83] | SUH, M. G., YANG, Q. F., YANG, K. Y., YI, X., and VAHALA, K. J. Microresonator soliton dual-comb spectroscopy. Science, 354, 600–603 (2016) |
| [84] | STEINMETZ, T., WILKEN, T., ARAUJO-HAUCK, C., HOLZWARTH, R., HANSCH, T. W., PASQUINI, L., MANESCAU, A., D’ODORICO, S., MURPHY, M. T., KENTISCHER, T., SCHMIDT, W., and UDEM, T. Laser frequency combs for astronomical observations. Science, 321, 1335–1337 (2008) |
| [85] | HU, Y., DING, S. L., QIN, Y. C., GU, J. X., WAN, W. J., XIAO, M., and JIANG, X. S. Generation of optical frequency comb via giant optomechanical oscillation. Physical Review Letters, 127, 134301 (2021) |
| [86] | MARIN-PALOMO, P., KEMAL, J. N., KARPOV, M., KORDTS, A., PFEIFLE, J., PFEIFFER, M. H. P., TROCHA, P., WOLF, S., BRASCH, V., ANDERSON, M. H., ROSENBERGER, R., VIJAYAN, K., FREUDE, W., KIPPENBERG, T. J., and KOOS, C. Microresonator-based solitons for massively parallel coherent optical communications. nature, 546, 274–279 (2017) |
| [87] | YU, M. J., OKAWACHI, Y., GRIFFITH, A. G., LIPSON, M., and GAETA, A. L. Microresonator-based high-resolution gas spectroscopy. Optics Letters, 42, 4442–4445 (2017) |
| [88] | SOYKAL, O. O., RUSKOV, R., and TAHAN, C. Sound-based analogue of cavity quantum electrodynamics in silicon. Physical Review Letters, 107, 235502 (2011) |
| [89] | CAO, L. S., QI, D. X., PENG, R. W., WANG, M., and SCHMELCHER, P. Phononic frequency combs through nonlinear resonances. Physical Review Letters, 112, 075505 (2014) |
| [90] | GANESAN, A., DO, C., and SESHIA, A. Phononic frequency comb via intrinsic three-wave mixing. Physical Review Letters, 118, 033903 (2017) |
| [91] | GANESAN, A., DO, C., and SESHIA, A. Phononic frequency comb via three-mode parametric three-wave mixing. Applied Physics Letters, 112, 021906 (2018) |
| [92] | GANESAN, A., DO, C., and SESHIA, A. Frequency transitions in phononic four-wave mixing. Applied Physics Letters, 111, 064101 (2017) |
| [93] | QI, Z., MENYUK, C. R., GORMAN, J. J., and GANESAN, A. Existence conditions for phononic frequency combs. Applied Physics Letters, 117, 183503 (2020) |
| [94] | CZAPLEWSKI, D. A., CHEN, C. Y., LOPEZ, D., SHOSHANI, O., ERIKSSON, A. M., STRACHAN, S., and SHAW, S. W. Bifurcation generated mechanical frequency comb. Physical Review Letters, 121, 244302 (2018) |
| [95] | SUN, J. K., YU, S., ZHANG, H. M., CHEN, D. Y., ZHOU, X., ZHAO, C., GERRARD, D. D., KWON, R., VUKASIN, G., XIAO, D. B., KENNY, T. W., WU, X. Z., and SESHIA, A. Generation and evolution of phononic frequency combs via coherent energy transfer between mechanical modes. Physical Review Applied, 19, 014031 (2023) |
| [96] | WU, J. H., SONG, P. H., ZANG, S., QIAO, Y., HUAN, R. H., ZHANG, W. M., and SHAO, L. Widely-tunable MEMS phononic frequency combs by multistage bifurcations under a single-tone excitation. Journal of Microelectromechanical Systems, 33, 384–394 (2024) |
| [97] | SONG, P. G., WU, J. H., ZANG, S. K., ABDEL-RAHMAN, E., SHAO, L., and ZHANG, W. M. Strong nonlinear mixing evolutions within phononic frequency combs. Communications in Nonlinear Science and Numerical Simulation, 138, 108233 (2024) |
| [98] | KUBENA, R. L., WALL, W. S., KOEHL, J., and JOYCE, R. J. Phononic comb generation in high-Q quartz resonators. Applied Physics Letters, 116, 053501 (2020) |
| [99] | ENAMUL-HOQUE-YOUSUF, S. M., LEE, J. S., SHAW, S. W., and FENG, X. L. Phononic frequency combs in atomically thin nanoelectromechanical resonators via 1:1 and 2:1 internal resonances. Journal of Microelectromechanical Systems, 32, 335–346 (2023) |
| [100] | LUO, W. Y., GAO, N. K., and LIU, D. Multimode nonlinear coupling induced by internal resonance in a microcantilever resonator. Nano Letters, 21, 1062–1067 (2021) |
| [101] | WANG, X. F., YANG, Q. Q., HUAN, R. H., SHI, Z., ZHU, W. Q., JIANG, Z. D., DENG, Z. C., and WEI, X. Y. Frequency comb in 1:3 internal resonance of coupled micromechanical resonators. Applied Physics Letters, 120, 173506 (2022) |
| [102] | BATISTA, A. A. and DE SOUZA, A. A. L. Frequency-comb response of a parametrically driven duffing oscillator to a small added ac excitation. Journal of Applied Physics, 128, 244901 (2020) |
| [103] | CHEN, H. Y., CHEN, D. Y., HUAN, R. H., FU, Y. Q., and XIE, J. Coherent phonon manipulation using single-mode circular electrostatic resonator. Sensors and Actuators A: Physical, 359, 114492 (2023) |
| [104] | YANG, Q. Q., WANG, X. F., HUAN, R. H., XU, L., XU, Y. T., JIANG, Z. D., and WEI, X. Y. Asymmetric phononic frequency comb in a rhombic micromechanical resonator. Applied Physics Letters, 118, 223502 (2021) |
| [105] | WANG, X. F., YANG, Q. Q., SHI, Z., HUAN, R. H., ZHU, W. Q., JING, X. J., DENG, Z. C., and WEI, X. Y. Frequency comb in a parametrically modulated micro-resonator. Acta Mechanica Sinica, 38, 521596 (2022) |
| [106] | HUSSEIN, H. M., KIM, S., RINALDI, M., ALÙ, A., and CASSELLA, C. Passive frequency comb generation at radiofrequency for ranging applications. Nature Communications, 15, 2844 (2024) |
| [107] | ANDERSON, P. W. Absence of diffusion in certain random lattices. Physical Review, 109, 1492 (1958) |
| [108] | RIGAL, B., DRAHI, D., JARLOV, C., DWIR, B., RUDRA, A., KULKOVA, I., LYASOTA, A., and KAPON, E. Probing disorder and mode localization in photonic crystal cavities using sitecontrolled quantum dots. Journal of Applied Physics, 123, 043109 (2018) |
| [109] | HANLEY, T. H., GALLACHER, B. J., and GRIGG, H. T. D. On the exploitation of mode localization in surface acoustic wave mems. Mechanical Systems and Signal Processing, 89, 27–36 (2017) |
| [110] | FISCHER, E. W., ANDERS, J., and SAALFRANK, P. Cavity-altered thermal isomerization rates and dynamical resonant localization in vibro-polaritonic chemistry. The Journal of Chemical Physics, 156, 154305 (2022) |
| [111] | CHEN, Y. Y., SONG, Z. G., and LI, F. M. Generating mechanism of mode localization for the beams and its application in the passive vibration control. Journal of Sound and Vibration, 485, 115531 (2020) |
| [112] | HODGES, C. H. and WOODHOUSE, J. Vibration isolation from irregularity in a nearly periodic structure: theory and measurements. The Journal of the Acoustical Society of America, 74, 894–905 (1983) |
| [113] | PIERRE, C., TANG, D. M., and DOWELL, E. H. Localized vibrations of disordered multispan beams-theory and experiment. AIAA Journal, 25, 1249–1257 (1987) |
| [114] | PIERRE, C. and CHA, P. D. Strong mode localization in nearly periodic disordered structures. AIAA Journal, 27, 227–241 (1989) |
| [115] | PIERRE, C. Mode localization and eigenvalue loci veering phenomena in disordered structures. Journal of Sound and Vibration, 126, 485–502 (1988) |
| [116] | ZHAO, C., MONTASERI, M. H., WOOD, G. S., PU, S. H., SESHIA, A. A., and KRAFT, M. A review on coupled MEMS resonators for sensing applications utilizing mode localization. Sensors and Actuators A: Physical, 249, 93–111 (2016) |
| [117] | PACHKAWADE, V. State-of-the-art in mode-localized MEMS coupled resonant sensors: a comprehensive review. IEEE Sensors Journal, 21, 8751–8779 (2021) |
| [118] | THIRUVENKATANATHAN, P., YAN, J. Z., WOODHOUSE, J., AZIZ, A., and SESHIA, A. A. Ultrasensitive mode-localized mass sensor with electrically tunable parametric sensitivity. Applied Physics Letters, 96, 081913 (2010) |
| [119] | ZHAO, C., WOOD, C. S., XIE, J. B., CHANG, H. L., PU, S. H., and KRAFT, M. A force sensor based on three weakly coupled resonators with ultrahigh sensitivity. Sensors and Actuators A: Physical, 232, 151–162 (2015) |
| [120] | THIRUVENKATANATHAN, P., YAN, J. Z., and ASESHIA, A. Common mode rejection in electrically coupled MEMS resonators utilizing mode localization for sensor applications. Joint Meeting of the 23rd European Frequency and Time Forum/IEEE International Frequency Control Symposium, Besancon (2009) |
| [121] | SPLETZER, M., RAMAN, A., WU, A. Q., XU, X. F., and REIFENBERGER, R. Ultrasensitive mass sensing using mode localization in coupled microcantilevers. Applied Physics Letters, 88, 254102 (2006) |
| [122] | SPLETZER, M., RAMAN, A., SUMALI, H., and SULLIVAN, J. P. Highly sensitive mass detection and identification using vibration localization in coupled microcantilever arrays. Applied Physics Letters, 92, 114102 (2008) |
| [123] | ZHANG, H. M., HUANG, J., YUAN, W. Z., and CHANG, H. L. A highsensitivity micromechanical electrometer based on mode localization of two degree-of-freedom weakly coupled resonators. Journal of Microelectromechanical Systems, 25, 937–946 (2016) |
| [124] | ZHANG, H. M., YANG, J., YUAN, W. Z., and CHANG, H. L. Linear sensing for mode-localized sensors. Sensors and Actuators A: Physical, 277, 35–42 (2018) |
| [125] | ZHANG, H. M., CHANG, H. L., and YUAN, W. Z. Characterization of forced localization of disordered weakly coupled micromechanical resonators. Microsystems & Nanoengineering, 3, 1–9 (2017) |
| [126] | YANG, J., ZHONG, J. M., and CHANG, H. L. A closed-loop mode-localized accelerometer. Journal of Microelectromechanical Systems, 27(2), 210–217 (2018) |
| [127] | LI, H., ZHANG, Z., ZU, L. H., HAO, Y. C., and CHANG, H. L. Micromechanical mode-localized electric current sensor. Microsystems & Nanoengineering, 8, 42 (2022) |
| [128] | WANG, K. F., XIONG, X. Y., WANG, Z., MA, L. G., WANG, B. W., YANG, W. H., BIE, X. R., LI, Z. T., and ZOU, X. D. A decouple-decomposition noise analysis model for closed-loop mode-localized tilt sensors. Microsystems & Nanoengineering, 9, 157 (2023) |
| [129] | ZHAO, C., WOOD, G. S., XIE, J. B., CHANG, H. L., PU, S. H., and KRAFT, M. A comparative study of output metrics for an MEMS resonant sensor consisting of three weakly coupled resonators. Journal of Microelectromechanical Systems, 25, 626–636 (2016) |
| [130] | ZHAO, C., WOOD, G. S., PU, S. H., and KRAFT, M. A mode-localized MEMS electrical potential sensor based on three electrically coupled resonators. Journal of Sensors and Sensor Systems, 6, 1–8 (2017) |
| [131] | WANG, D. F., ZHOU, D., LIU, S. Y., and HONG, J. Localized trio cantilevers for identifying different mass perturbations. Microsystem Technologies, 25, 2993–3003 (2019) |
| [132] | PENG, B., HU, K. M., SHAO, L., YAN, H., LI, L., WEI, X. Y., and ZHANG, W. M. A sensitivity tunable accelerometer based on series-parallel electromechanically coupled resonators using mode localization. Journal of Microelectromechanical Systems, 29, 3–13 (2019) |
| [133] | ZHANG, H. M., PANDIT, M., SOBREVIELA, G., PARAJULI, M., CHEN, D. Y., SUN, J. K., ZHAO, C., and SESHIA, A. A. Mode-localized accelerometer in the nonlinear duffing regime with 75 ng bias instability and 95 ng/Hz noise floor. Microsystems & Nanoengineering, 8, 17 (2022) |
| [134] | LIU, Z. H., CHEN, Y. Z., WANG, X. F., XU, Y. T., DAI, H. S., SHI, Z., WAN, H. B., WEI, X. Y., and HUAN, R. H. Nonlinearity enhanced mode localization in two coupled mems resonators. International Journal of Mechanical Sciences, 271, 109133 (2024) |
| [135] | ZHAO, C., SOBREVIELA, G., PANDIT, M., DU, S. J., ZOU, X. D., and SESHIA, A. Experimental observation of noise reduction in weakly coupled nonlinear mems resonators. Journal of Microelectromechanical Systems, 26, 1196–1203 (2017) |
| [136] | LYU, M., ZHAO, J., KACEM, N., SONG, J. H., FAN, K. F., LIU, P. G., and HUANG, Y. Nonlinearity modulation in a mode-localized mass sensor based on electrostatically coupled resonators under primary and superharmonic resonances. Physica Scripta, 98, 045217 (2023) |
| [137] | LIU, X. J., HU, H. Y., WANG, X., LIU, R. M., YIN, J., and WANG, L. F. Vibration transfer in spatially separated thin-film graphene resonators. ACS Applied Nano Materials, 7, 18779–18785 (2024) |
| [1] | Zeyu CHAI, J. T. HAN, Xuyuan SONG, Jian ZANG, Yewei ZHANG, Zhen ZHANG. Theoretical and experimental investigations on an X-shaped vibration isolator with active controlled variable stiffness [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(8): 1371-1386. |
| [2] | Runqing CAO, Zilong GUO, Wei CHEN, Huliang DAI, Lin WANG. Nonlinear dynamics of a circular curved cantilevered pipe conveying pulsating fluid based on the geometrically exact model [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 261-276. |
| [3] | Xin FAN, Changan ZHU, Xiaoye MAO, Hu DING. Adjacent mode resonance of a hydraulic pipe system consisting of parallel pipes coupled at middle points [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(3): 363-380. |
| [4] | Yaode YIN, Demin ZHAO, Jianlin LIU, Zengyao XU. Nonlinear dynamic analysis of dielectric elastomer membrane with electrostriction [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(6): 793-812. |
| [5] | Lei LI, Hanbiao LIU, Jianxin HAN, Wenming ZHANG. Nonlinear modal coupling in a T-shaped piezoelectric resonator induced by stiffness hardening effect [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(6): 777-792. |
| [6] | Duquan ZUO, B. SAFAEI, S. SAHMANI, Guoling MA. Nonlinear free vibrations of porous composite microplates incorporating various microstructural-dependent strain gradient tensors [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(6): 825-844. |
| [7] | Lei XIA, Jiaojiao SUN, Zuguang YING, Ronghua HUAN, Weiqiu ZHU. Dynamics and response reshaping of nonlinear predator-prey system undergoing random abrupt disturbances [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(8): 1123-1134. |
| [8] | Kun ZHOU, Qiao NI, Wei CHEN, Huliang DAI, Zerui PENG, Lin WANG. New insight into the stability and dynamics of fluid-conveying supported pipes with small geometric imperfections [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(5): 703-720. |
| [9] | A. SARAFRAZ, S. SAHMANI, M. M. AGHDAM. Nonlinear primary resonance analysis of nanoshells including vibrational mode interactions based on the surface elasticity theory [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(2): 233-260. |
| [10] | Yunyue CONG, Houjun KANG, Tieding GUO. Analysis of in-plane 1:1:1 internal resonance of a double cable-stayed shallow arch model with cables' external excitations [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(7): 977-1000. |
| [11] | Houjun KANG, Tieding GUO, Weidong ZHU, Junyi SU, Bingyu ZHAO. Dynamical modeling and non-planar coupled behavior of inclined CFRP cables under simultaneous internal and external resonances [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(5): 649-678. |
| [12] | Nan ZHANG, Bin CHENG, Hexi BAOYIN. A new physical model on the capillary phenomenon of granular particles [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(1): 127-138. |
| [13] | Kuan LU, Yushu CHEN, Lei HOU. Bifurcation characteristics analysis of a class of nonlinear dynamical systems based on singularity theory [J]. Applied Mathematics and Mechanics (English Edition), 2017, 38(9): 1233-1246. |
| [14] | Minghui FU, Kelang LU, Weihua LI, S. V. SHESHENIN. New way to construct high order Hamiltonian variational integrators [J]. Applied Mathematics and Mechanics (English Edition), 2016, 37(8): 1041-1052. |
| [15] | Bensong YU, Dongping JIN, Hao WEN. Nonlinear dynamics of flexible tethered satellite system subject to space environment [J]. Applied Mathematics and Mechanics (English Edition), 2016, 37(4): 485-500. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS