Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (2): 269-288.doi: https://doi.org/10.1007/s10483-025-3212-7
Previous Articles Next Articles
Received:2024-09-27
Revised:2024-12-07
Online:2025-02-03
Published:2025-02-02
Contact:
S. H. JO, E-mail: soohojo@dgu.ac.krSupported by:2010 MSC Number:
S. H. JO. Concurrent generation and amplification of longitudinal and bending waves using defective phononic crystals. Applied Mathematics and Mechanics (English Edition), 2025, 46(2): 269-288.
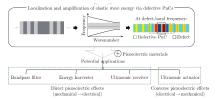
Fig. 1
A brief illustration of the phenomenon of localization and amplification of elastic wave energy via defective PnCs and their potential applications to bandpass filters, energy harvesters, ultrasonic receivers, and ultrasonic actuators when the defective PnCs are combined with piezoelectric materials (color online)"
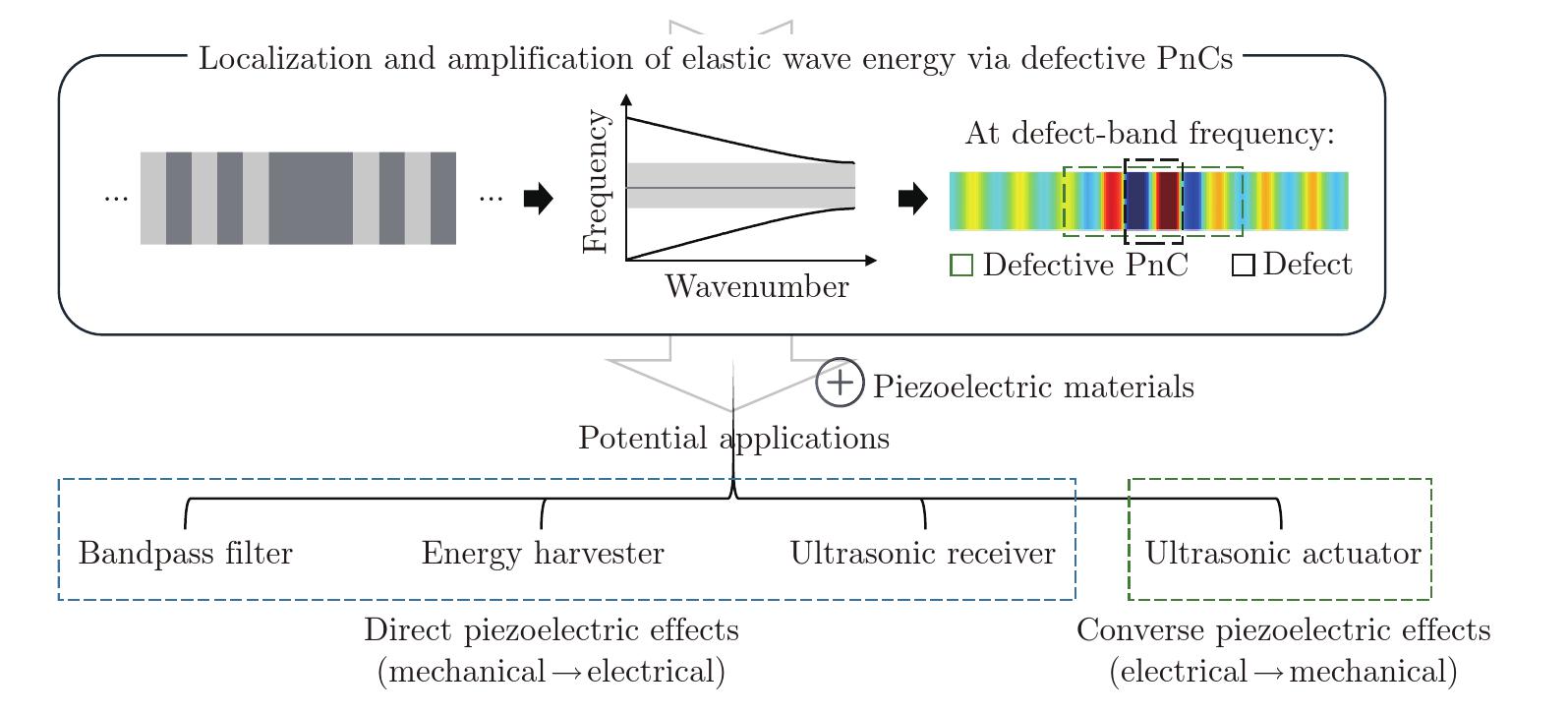

Fig. 2
An overview of previous research on the use of defective PnCs integrated with piezoelectric materials for excitation of either longitudinal or bending waves, with a particular focus on the amplification of velocity amplitudes. The research trend begins with single defect scenarios under longitudinal waves and progresses to double defect scenarios under bending waves (color online)"
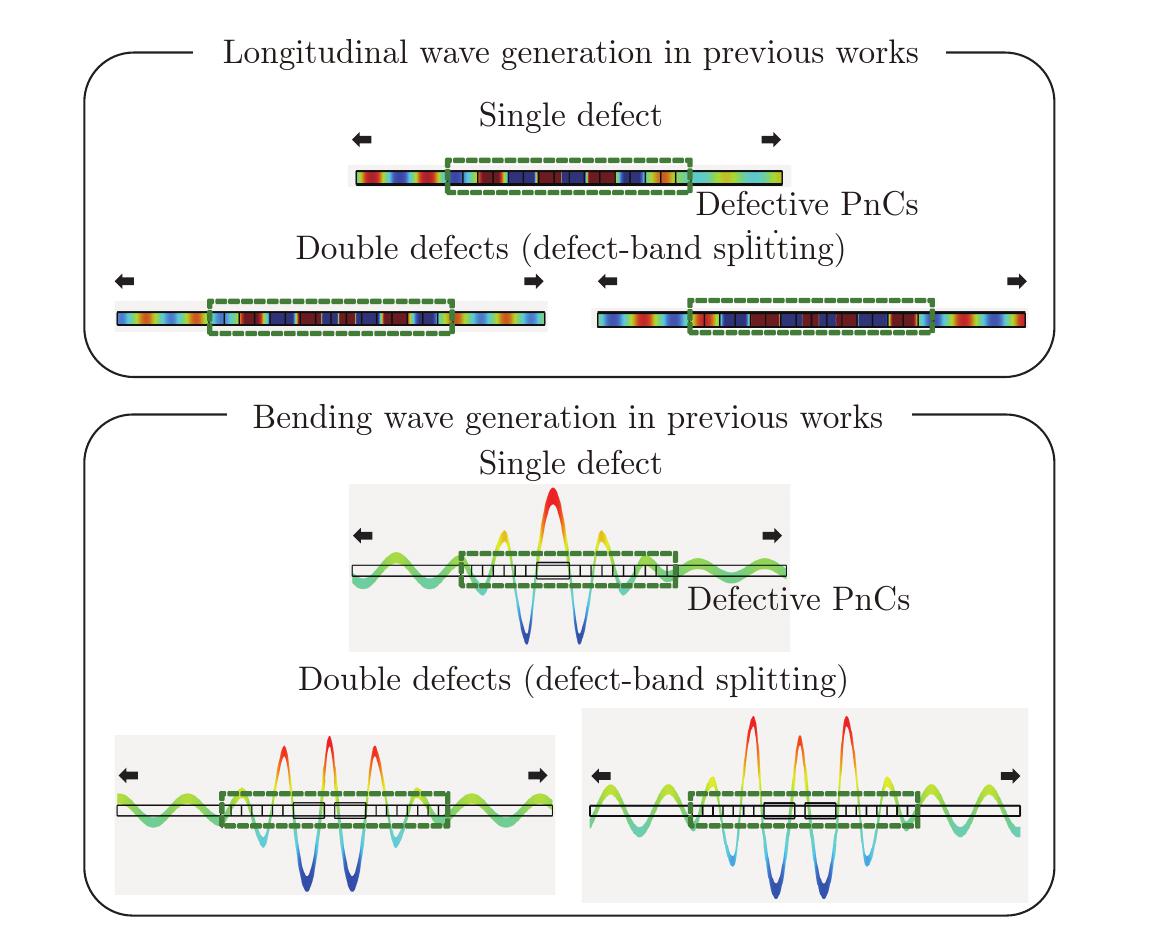

Fig. 3
The front view of the targeted concurrent wave-generation system that consists of a one-dimensional defective PnC with bimorph piezoelectric elements connected to two independent voltage sources vPT and vPB. The defective PnC is employed in band-structure analysis, whereas the defective PnC attached to semi-infinite structures is utilized in wave-generation analysis (color online)"
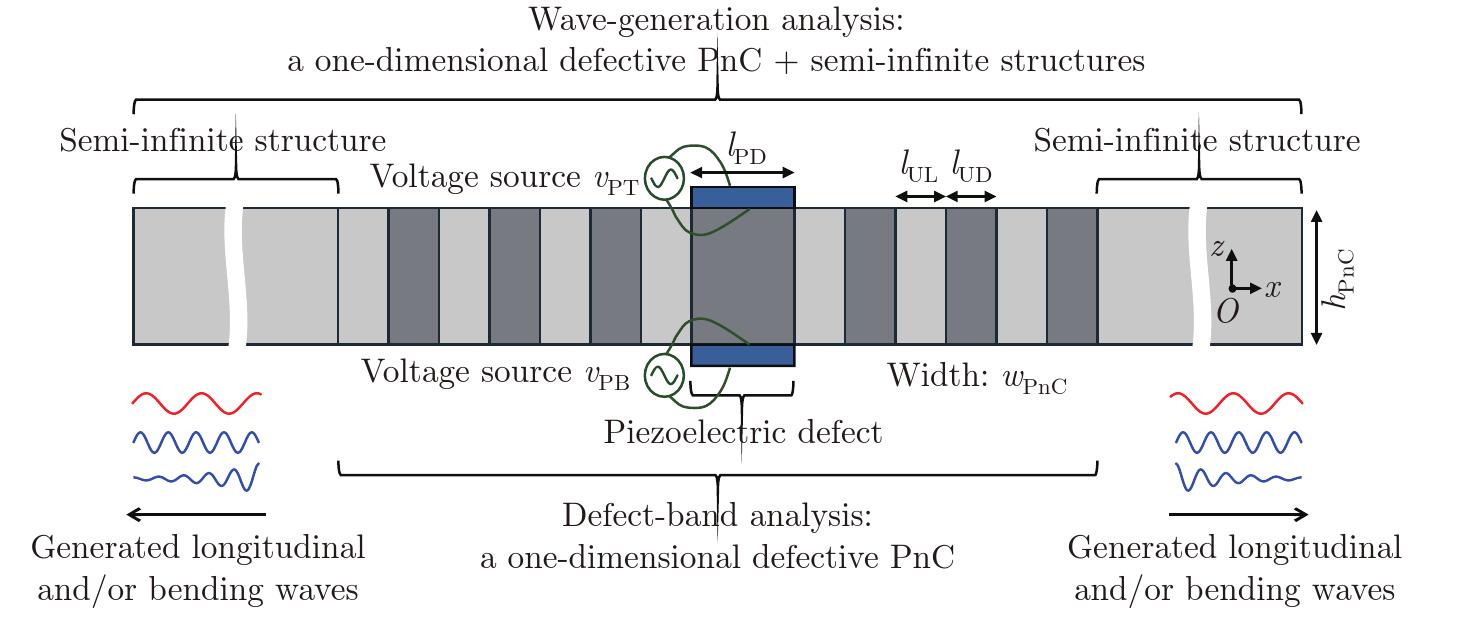

Fig. 4
Intuitive illustration of band-structure analysis at the unit cell and defective PnC levels: (a) the transfer matrix method for band-gap analysis at the unit-cell level, (b) the transfer matrix method for defect-band analysis at the defective PnC level, and (c) the sequential results expected, including band-gap frequencies, defect-band frequencies, and defect-mode shapes (color online)"
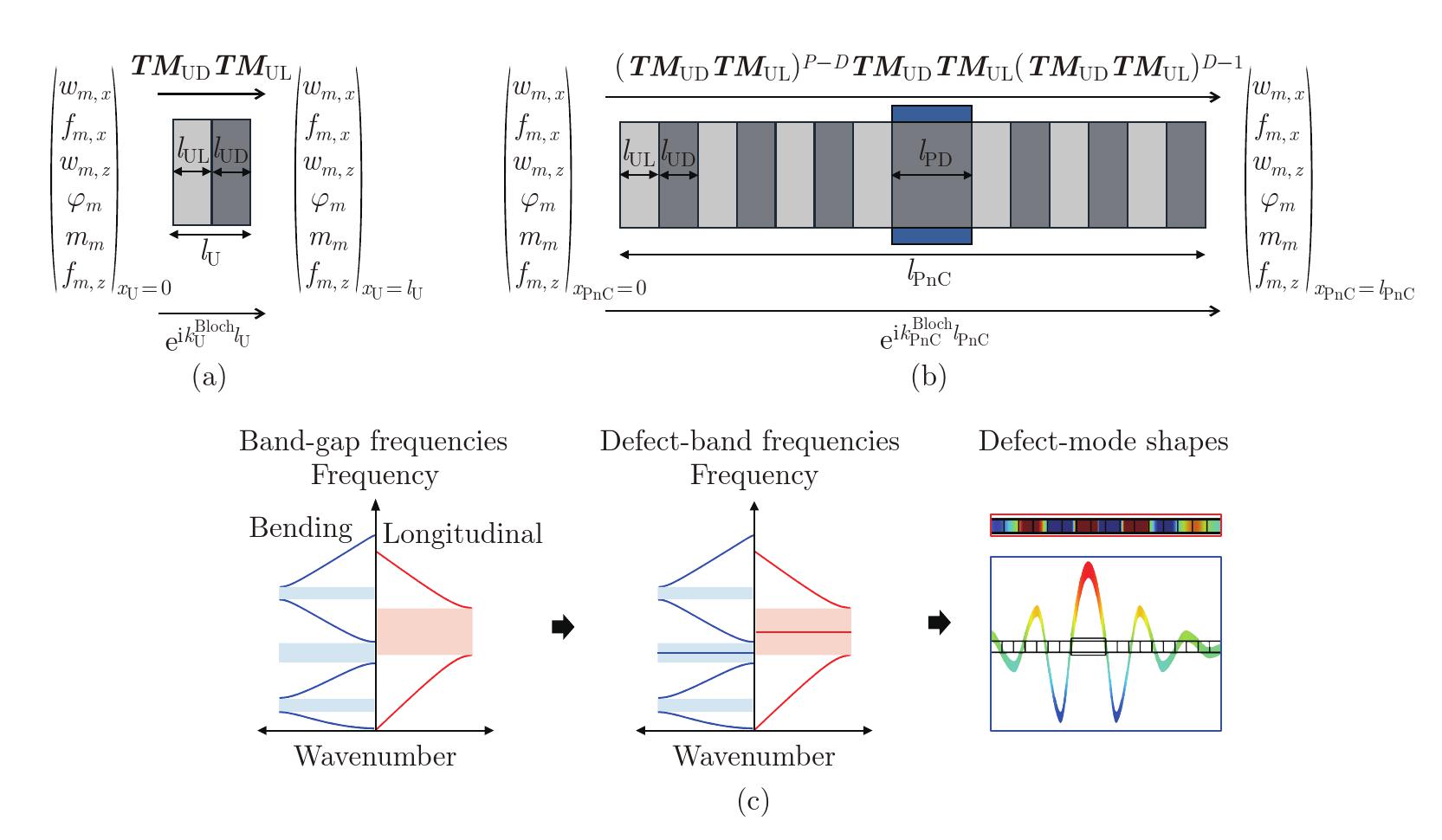

Fig. 5
Intuitive illustration of wave-generation analysis at the system level: (a) the S-parameter method, which considers two input voltage sources, to predict the velocity amplitude of outgoing waves and (b) the sequential results expected, including the velocity-amplitude frequency response curves and the effects of temporal phase difference and voltage magnitude difference on peak velocity amplitudes (color online)"
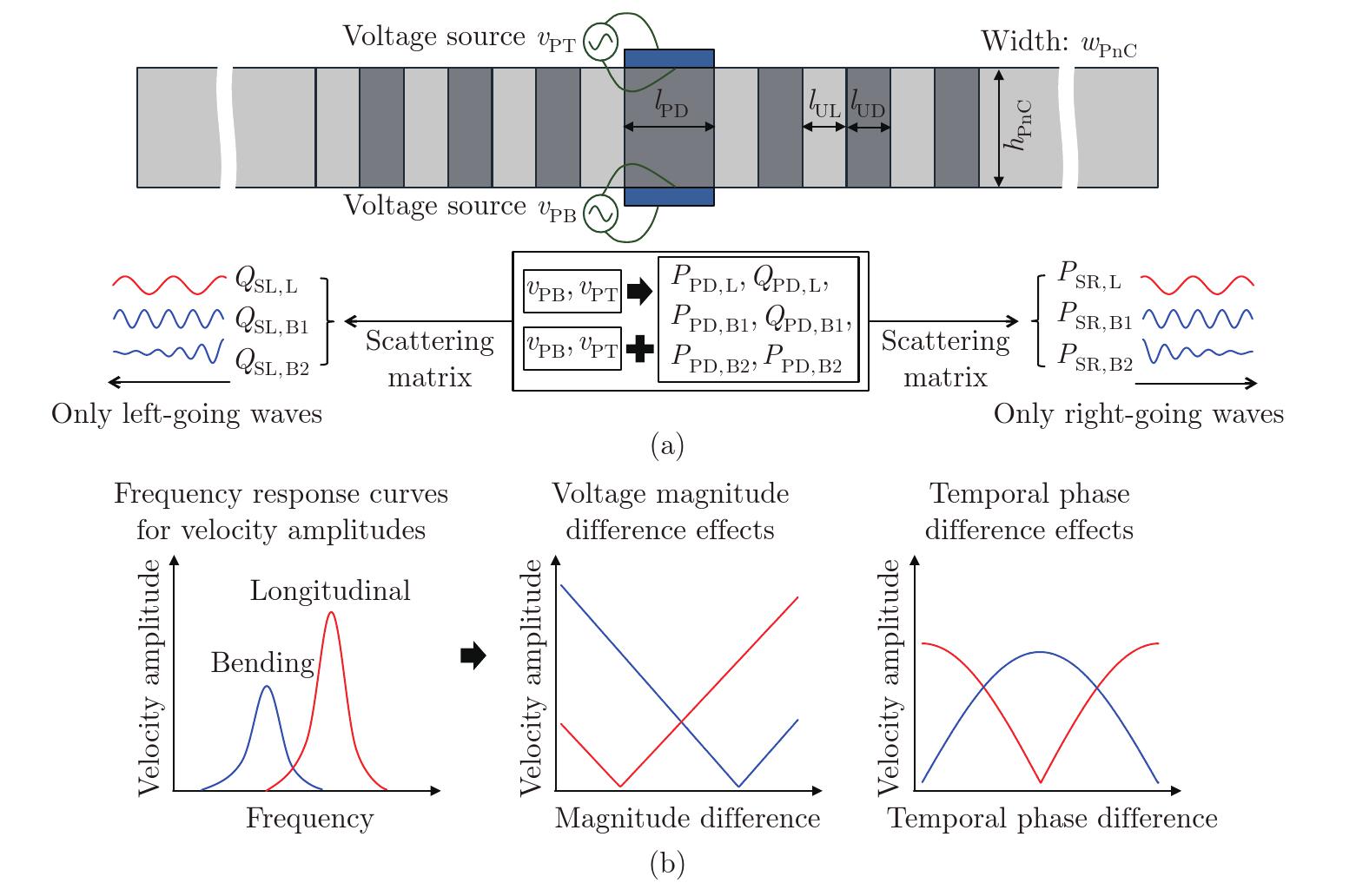

Fig. 6
Results of the band-structure analysis. The x-axes in (a) and (b) correspond to the real and imaginary parts of the normalized Bloch wavenumber, respectively. The solid red and blue lines indicate the results obtained from the proposed analytical model for longitudinal and bending waves, respectively. In contrast, the results from the COMSOL simulation are depicted using the black dashed lines. The phononic band gaps identified at the unit-cell level are highlighted with boxes, and the lines within these boxes indicate the defect bands identified at the defective PnC level (color online)"
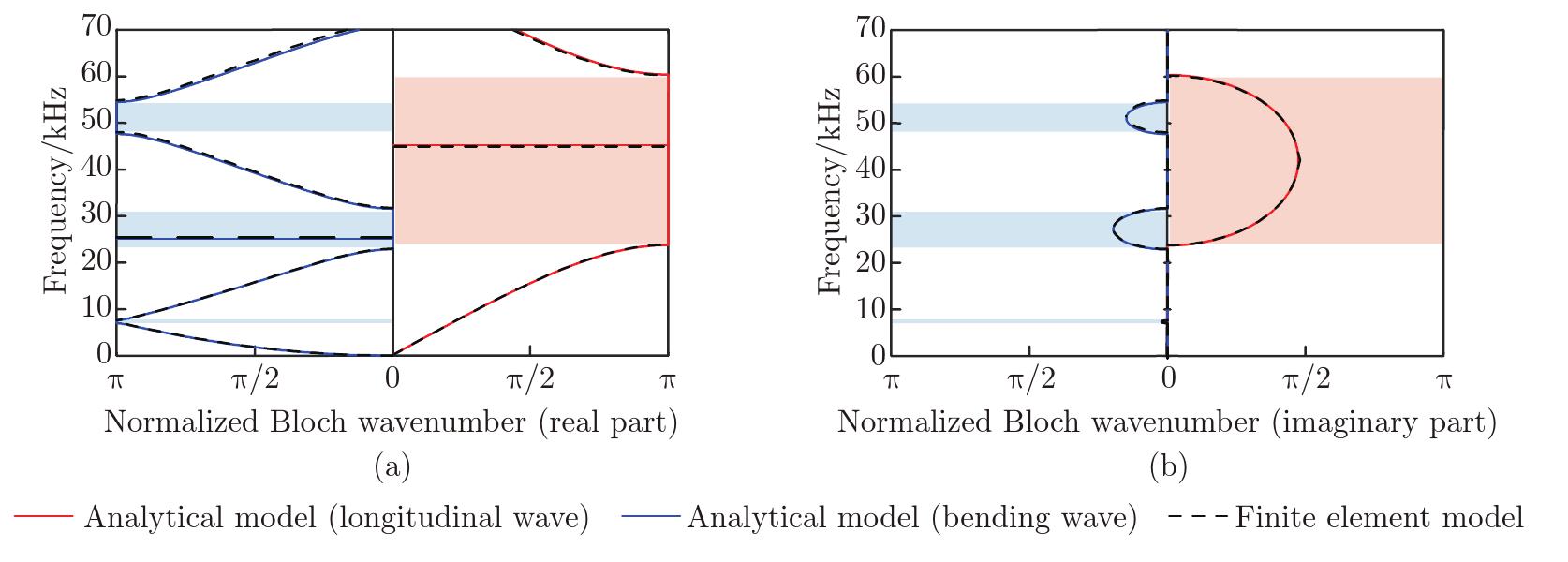

Fig. 7
Results of the defect-mode-shape analysis: (a) the axial displacement field under longitudinal waves, (b) the transverse displacement field under bending waves, (c) the axial strain field under longitudinal waves, and (d) the axial strain field under bending waves. In (c), the strain field is determined at zPnC=0. In (d), the strain field is determined at zPnC=hPnC/2 (color online)"
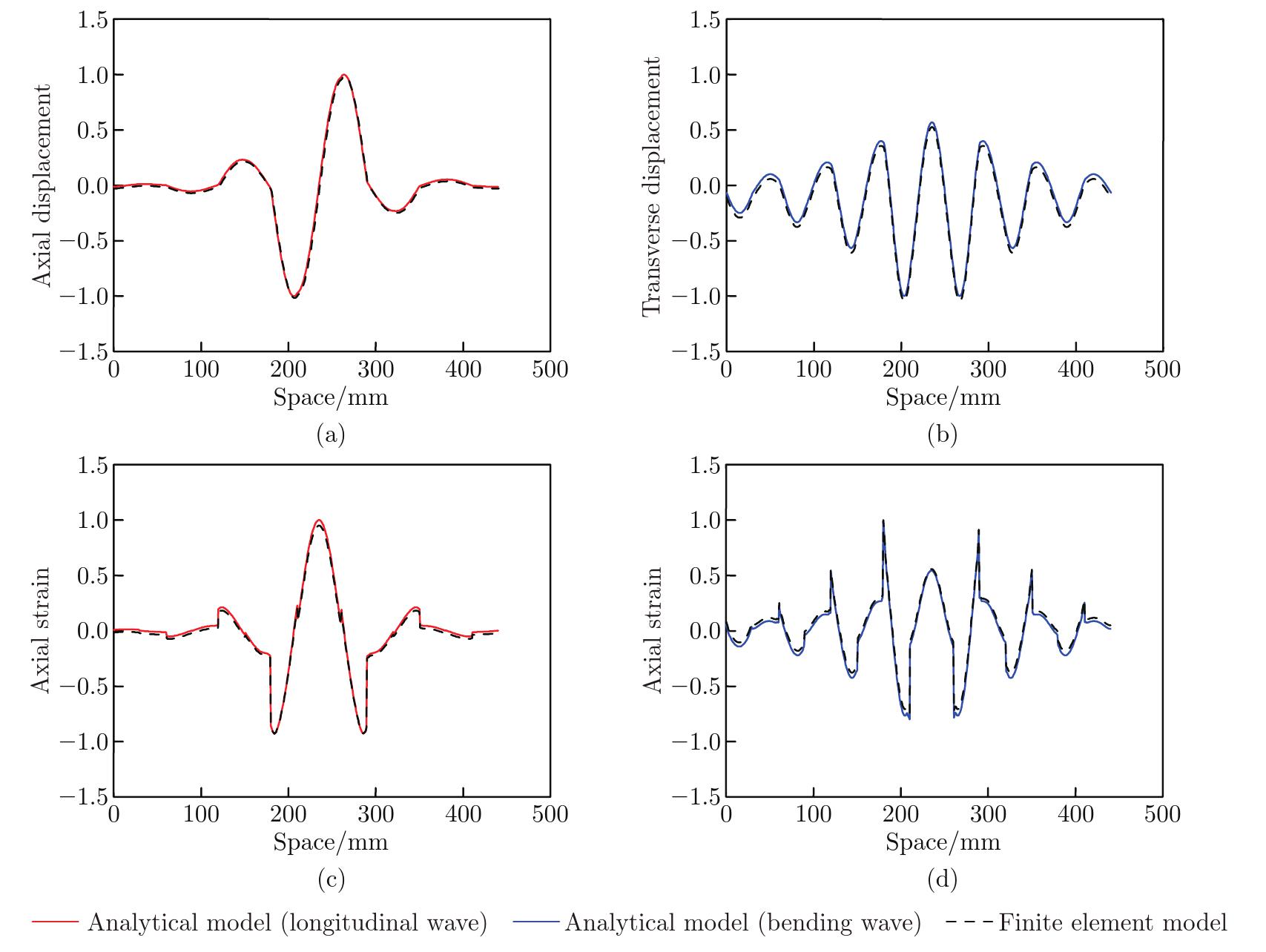

Fig. 8
Results of the wave-generation analysis: the frequency response curves for (a) the axial velocity amplitudes when (vPT, vPB)=(1 V, 1 V), (b) the transverse velocity amplitudes when (vPT, vPB)=(1 V, −1 V), (c) the axial velocity amplitudes and (d) the transverse velocity amplitudes when (vPT, vPB)=(1 V, 0 V) (color online)"
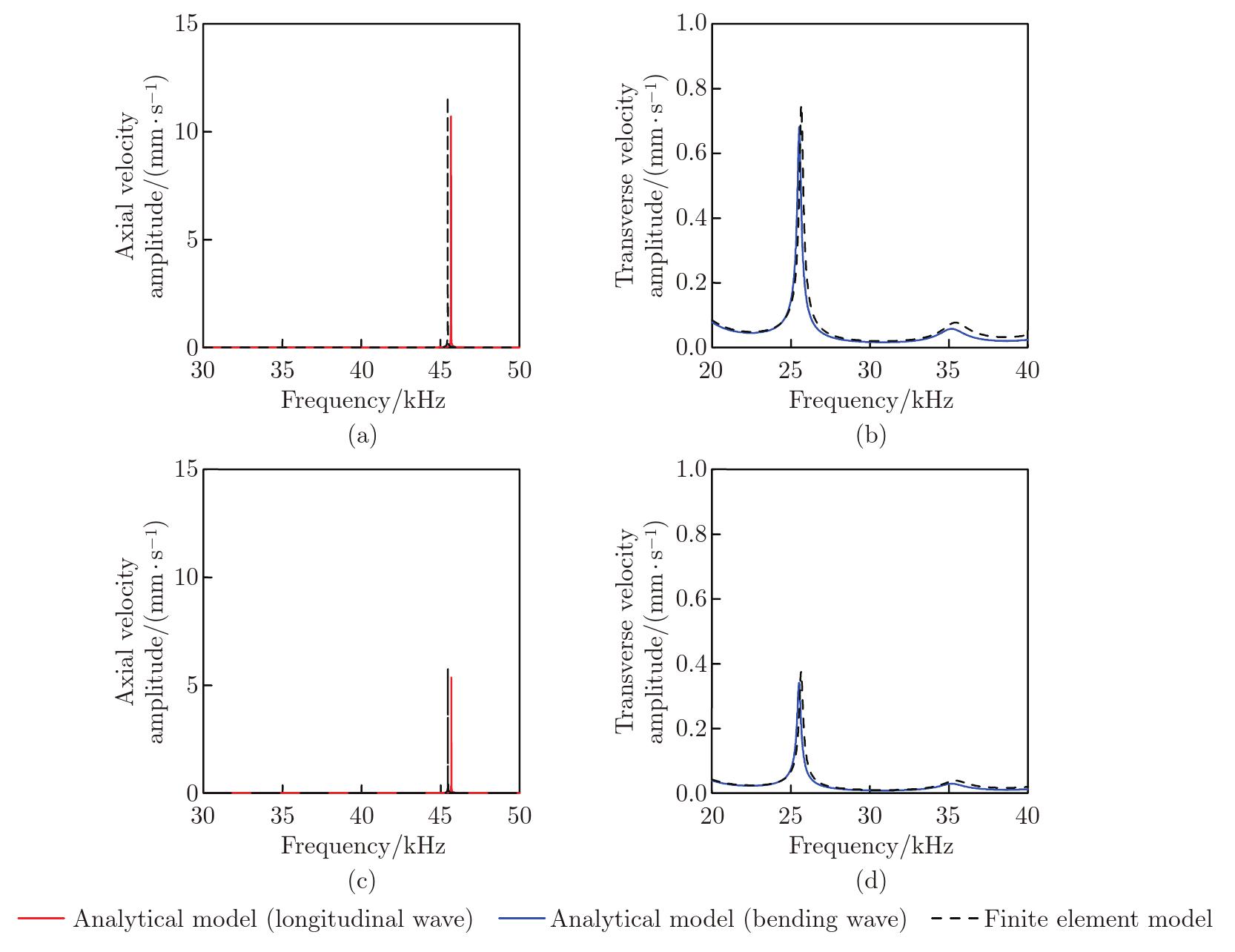

Fig. 9
Results of the parametric study when the magnitude and temporal phase differences are examined separately: the effects of (a) the magnitude difference and (b) the temporal phase difference on the axial (45.68 kHz) and transverse (25.51 kHz) velocity amplitudes. In (a), a temporal phase difference of 0 is present. Conversely, in (b), a magnitude difference of 1 V is present (color online)"
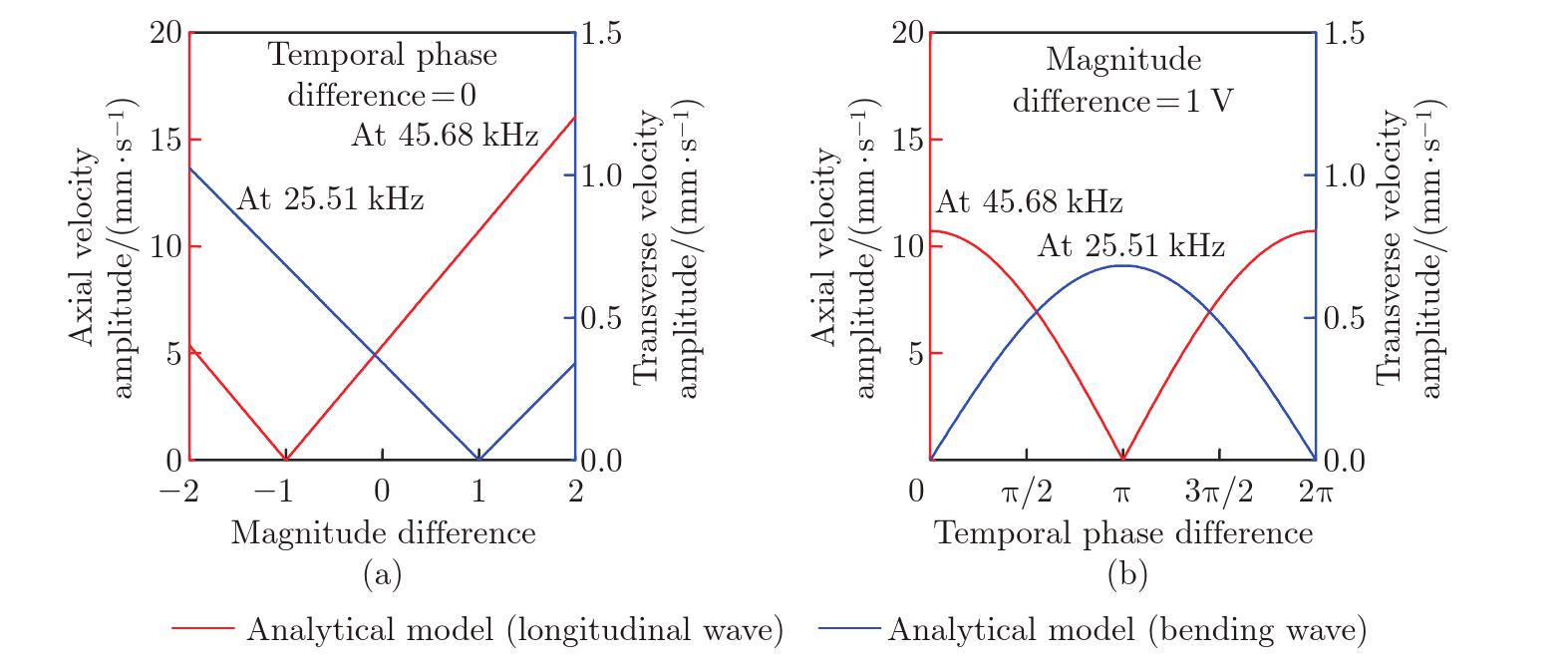

Fig. 10
Results of the parametric study when the magnitude and temporal phase differences are coupled: the effects of (a) the magnitude difference and (b) the temporal phase difference on the axial (45.68 kHz) and transverse (25.51 kHz) velocity amplitudes. In (a), a temporal phase difference of π/4 is present. Conversely, in (b), a magnitude difference of 2V is present (color online)"

| [1] | LIU, C. X. and YU, G. L. Deep learning for the design of phononic crystals and elastic metamaterials. Journal of Computational Design and Engineering, 10, 602–614 (2023) |
| [2] | OUDICH, M., KONG, X., ZHANG, T., QIU, C., and JING, Y. Engineered Moiré photonic and phononic superlattices. Nature Materials, 23, 1169–1178 (2024) |
| [3] | AKBARI-FARAHANI, F. and EBRAHIMI-NEJAD, S. From defect mode to topological metamaterials: a state-of-the-art review of phononic crystals & acoustic metamaterials for energy harvesting. Sensors and Actuators A: Physical, 365, 114871 (2024) |
| [4] | LEE, G., LEE, D., PARK, J., JANG, Y., KIM, M., and RHO, J. Piezoelectric energy harvesting using mechanical metamaterials and phononic crystals. Communications Physics, 5, 94 (2022) |
| [5] | MA, H., LIU, H., CONG, Y., and GU, S. Band gap study of periodic piezoelectric micro-composite laminated plates by finite element method and its application in feedback control. Mechanics of Materials, 195, 105029 (2024) |
| [6] | BAI, Y., LI, X., ZHOU, X., LI, P., and BEER, M. Soil-expended seismic metamaterial with ultralow and wide bandgap. Mechanics of Materials, 180, 104601 (2023) |
| [7] | JIN, J., HU, N., and HU, H. Size effects on the mixed modes and defect modes for a nano-scale phononic crystal slab. Applied Mathematics and Mechanics (English Edition), 44(1), 21–34 (2023) https://doi.org/10.1007/s10483-023-2945-6 |
| [8] | CHUANG, K. C., ZHANG, Z. Q., and WANG, H. X. Experimental study on slow flexural waves around the defect modes in a phononic crystal beam using fiber bragg gratings. Physics Letters A, 380, 3963–3969 (2016) |
| [9] | XIAO, J., DING, X., HUANG, W., HE, Q., and SHAO, Y. Rotating machinery weak fault features enhancement via line-defect phononic crystal sensing. Mechanical Systems and Signal Processing, 220, 111657 (2024) |
| [10] | LEE, D., YOUN, B. D., and JO, S. H. Deep-learning-based framework for inverse design of a defective phononic crystal for narrowband filtering. International Journal of Mechanical Sciences, 255, 108474 (2023) |
| [11] | EL-KADMIRI, I., BEN-ALI, Y., ERROUAS, Y., KHALED, A., and BRIA, D. Multi-channel filters with high performance based on the creation of a geometrical defect in 1D phononic star waveguides structure. Materials Today: Proceedings, 45, 7576–7583 (2021) |
| [12] | GENG, Q., WANG, T., WU, L., and LI, Y. Defect coupling behavior and flexural wave energy harvesting of phononic crystal beams with double defects in thermal environments. Journal of Physics D: Applied Physics, 54, 225501 (2021) |
| [13] | CAO, Z., WANG, K., and WANG, B. Energy harvesting performance of acoustic energy harvesters consisting of flexoelectric plates and defect-state phononic crystals. Journal of Vibration Engineering & Technologies, 12, 5101–5117 (2024) |
| [14] | SHU, Z., ZHANG, G., CONG, Y., and GU, S. Size effects on a one-dimensional defective phononic crystal sensor. Smart Materials and Structures, 32, 115029 (2023) |
| [15] | XIAO, J. W., DING, X. X., WANG, Y. Q., HUANG, W. B., HE, Q. B., and SHAO, Y. M. Gear fault detection via directional enhancement of phononic crystal resonators. International Journal of Mechanical Sciences, 276, 109453 (2024) |
| [16] | JO, S. H., PARK, M., KIM, M., and YANG, J. Tunable bandpass filters using a defective phononic crystal shunted to synthetic negative capacitance for longitudinal waves. Journal of Applied Physics, 135, 164502 (2024) |
| [17] | JO, S. H. Electrically controllable behaviors in defective phononic crystals with inductive-resistive circuits. International Journal of Mechanical Sciences, 278, 109485 (2024) |
| [18] | JO, S. H. and YOUN, B. D. An explicit solution for the design of a target-frequency-customized, piezoelectric-defect-introduced phononic crystal for elastic wave energy harvesting. Journal of Applied Physics, 130, 184902 (2021) |
| [19] | JO, S. H. and YOUN, B. D. An improved analytical model that considers lateral effects of a phononic crystal with a piezoelectric defect for elastic wave energy harvesting. International Journal of Mechanical Sciences, 205, 106593 (2021) |
| [20] | WANG, K., LI, X. S., CAO, L., GUO, P. Y., FAN, G. T., QIN, I. J., and MA, T. X. Enhancement of piezoelectric energy harvesting for flexural waves by a metasurfaceassisted phononic cavity. Results in Physics, 63, 107870 (2024) |
| [21] | ZHANG, G. Y., HE, Z. Z., WANG, S. P., HONG, J., CONG, Y., and GU, S. T. Elastic foundation-introduced defective phononic crystals for tunable energy harvesting. Mechanics of Materials, 191, 104909 (2024) |
| [22] | YANG, X. E., ZHONG, J. H., and XIANG, J. W. Designing a phononic crystal with a large defect to enhance elastic wave energy localization and harvesting. Japanese Journal of Applied Physics, 61, 017002 (2022) |
| [23] | HOSSEINKHANI, A., EBRAHIMIAN, F., YOUNESIAN, D., and MOAYEDIZADEH, A. Defected metalattice structures for the enhanced localized vibrational energy harvesting. Nano Energy, 100, 107488 (2022) |
| [24] | LEE, G., PARK, J., CHOI, W., JI, B., KIM, M., and RHO, J. Multiband elastic wave energy localization for highly amplified piezoelectric energy harvesting using trampoline metamaterials. Mechanical Systems and Signal Processing, 200, 110593 (2023) |
| [25] | JO, S. H. and YOUN, B. D. Enhanced ultrasonic wave generation using energy-localized behaviors of phononic crystals. International Journal of Mechanical Sciences, 228, 107483 (2022) |
| [26] | JO, S. H., LEE, D., YOON, H., and YOUN, B. D. Double piezoelectric defects in phononic crystals for ultrasonic transducers. Journal of Physics D: Applied Physics, 56, 074002 (2023) |
| [27] | JO, S. H. and LEE, D. Flexural-wave-generation using a phononic crystal with a piezoelectric defect. Applied Mathematics and Mechanics (English Edition), 44(8), 1241–1262 (2023) https://doi.org/10.1007/s10483-023-3015-7 |
| [28] | JO, S. H. and LEE, D. An improved analytical model of a thick defective phononic crystal for bending wave excitation. International Journal of Mechanical Sciences, 264, 108822 (2024) |
| [29] | JO, S. H., LEE, D., and YOUN, B. D. Defect-band splitting of a one-dimensional phononic crystal with double defects for bending-wave excitation. Mathematics, 11, 3852 (2023) |
| [30] | SHEN, W., CONG, Y., GU, S., YIN, H., and ZHANG, G. A generalized supercell model of defect-introduced phononic crystal microplates. Acta Mechanica, 235, 1345–1360 (2024) |
| [31] | GENG, Q., FONG, P. K., NING, J., SHAO, Z., and LI, Y. Thermally-induced transitions of multi-frequency defect wave localization and energy harvesting of phononic crystal plate. International Journal of Mechanical Sciences, 222, 107253 (2022) |
| [32] | ERTURK, A. Assumed-modes modeling of piezoelectric energy harvesters: Euler-Bernoulli, Rayleigh, and Timoshenko models with axial deformations. Computers & Structures, 106, 214–227 (2012) |
| [33] | DIETL, J., WICKENHEISER, A., and GARCIA, E. A Timoshenko beam model for cantilevered piezoelectric energy harvesters. Smart Materials and Structures, 19, 055018 (2010) |
| [34] | MA, T. X., FAN, Q. S., ZHANG, C., and WANG, Y. S. Acoustic flatbands in phononic crystal defect lattices. Journal of Applied Physics, 129, 145104 (2021) |
| [35] | MA, T. X., FAN, Q. S., LI, Z. Y., ZHANG, C., and WANG, Y. S. Flexural wave energy harvesting by multi-mode elastic metamaterial cavities. Extreme Mechanics Letters, 41, 101073 (2020) |
| [36] | MA, T. X., LIU, J., ZHANG, C., and WANG, Y. S. Topological edge and interface states in phoxonic crystal cavity chains. Physical Review A, 106, 043504 (2022) |
| [37] | JO, S. H., YOON, H., SHIN, Y. C., and YOUN, B. D. Revealing defect-mode-enabled energy localization mechanisms of a one-dimensional phononic crystal. International Journal of Mechanical Sciences, 215, 106950 (2022) |
| [38] | LEE, W., LEE, J., PARK, C. I., and KIM, Y. Y. Polarization-independent full mode-converting elastic metasurfaces. International Journal of Mechanical Sciences, 266, 108975 (2024) |
| [39] | OH, Y. B., KIM, S. Y., CHO, S. H., LEE, J. S., and KIM, Y. Y. Near-perfect retroreflection of flexural waves via optimized elastic metagratings. International Journal of Mechanical Sciences, 262, 108750 (2024) |
| [40] | LEE, S. and YOUN, B. D. A new piezoelectric energy harvesting design concept: multimodal energy harvesting skin. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 131, 011010 (2009) |
| [41] | ERTURK, A., TARAZAGA, P. A., FARMER, J. R., and INMAN, D. J. Effect of strain nodes and electrode configuration on piezoelectric energy harvesting from cantilevered beams. Journal of Vibration and Acoustics, 58, 629–645 (2011) |
| [42] | LAUDE, V., ACHAOUI, Y., BENCHABANE, S., and KHELIF, A. Evanescent Bloch waves and the complex band structure of phononic crystals. Physical Review B: Condensed Matter and Materials Physics, 80, 092301 (2009) |
| [43] | MA, T. X. and CAO, L. Complex dispersion analysis of true and pseudo surface waves propagating in two-dimensional viscoelastic seismic metamaterials. AIP Advances, 14, 015219 (2024) |
| [44] | MA, T. X., FAN, Q. S., ZHANG, C., and WANG, Y. S. Flexural wave energy harvesting by the topological interface state of a phononic crystal beam. Extreme Mechanics Letters, 50, 101578 (2022) |
| [45] | JO, S. H., YOON, H., SHIN, Y. C., and YOUN, B. D. Revealing defect-mode-enabled energy localization mechanisms of a one-dimensional phononic crystal. International Journal of Mechanical Sciences, 215, 106950 (2022) |
| [1] | Wenkai ZHANG, C. S. LU, Minghao ZHAO, Cuiying FAN, Huayang DANG. On the interfacial behavior of a one-dimensional hexagonal piezoelectric quasicrystal film based on the beam theory [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(2): 289-304. |
| [2] | Jie CHEN, Xinyue ZHANG, Mingyang FAN. Dynamic behaviors of graphene platelets-reinforced metal foam piezoelectric beams with velocity feedback control [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(1): 63-80. |
| [3] | Lingyun GUO, Yizhan YANG, Wanli YANG, Yuantai HU. The action mechanism of the work done by the electric field force on moving charges to stimulate the emergence of carrier generation/recombination in a PN junction [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(6): 1001-1014. |
| [4] | Yu TAN, Fan PENG, Chang LIU, Daiming PENG, Xiangyu LI. Fourth-order phase-field modeling for brittle fracture in piezoelectric materials [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(5): 837-856. |
| [5] | Shijing GAO, Lele ZHANG, Jinxi LIU, Guoquan NIE, Weiqiu CHEN. Indentation behavior of a semi-infinite piezoelectric semiconductor under a rigid flat-ended cylindrical indenter [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(4): 649-662. |
| [6] | Xin FENG, Liaoliang KE, Yang GAO. Love wave propagation in one-dimensional piezoelectric quasicrystal multilayered nanoplates with surface effects [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(4): 619-632. |
| [7] | Shuangpeng LI, Ruoran CHENG, Nannan MA, Chunli ZHANG. Analysis of piezoelectric semiconductor fibers under gradient temperature changes [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 311-320. |
| [8] | Zhi LI, Cuiying FAN, Mingkai GUO, Guoshuai QIN, Chunsheng LU, Dongying LIU, Minghao ZHAO. Natural frequency analysis of laminated piezoelectric beams with arbitrary polarization directions [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(11): 1949-1964. |
| [9] | Jiawei MAO, Hao GAO, Junzhe ZHU, Penglin GAO, Yegao QU. Analytical modeling of piezoelectric meta-beams with unidirectional circuit for broadband vibration attenuation [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1665-1684. |
| [10] | N. SHAHVEISI, S. FELI. Dynamic and electrical responses of a curved sandwich beam with glass reinforced laminate layers and a pliable core in the presence of a piezoelectric layer under low-velocity impact [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(1): 155-178. |
| [11] | Yuan YANG, Nenghui ZHANG, Hanlin LIU, Jiawei LING, Zouqing TAN. Piezoelectric and flexoelectric effects of DNA adsorbed films on microcantilevers [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1547-1562. |
| [12] | Xueqian FANG, Qilin HE, Hongwei MA, Changsong ZHU. Multi-field coupling and free vibration of a sandwiched functionally-graded piezoelectric semiconductor plate [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(8): 1351-1366. |
| [13] | Youqi ZHANG, Rongyu XIA, Jie XU, Kefu HUANG, Zheng LI. Theoretical analysis of surface waves in piezoelectric medium with periodic shunting circuits [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(8): 1287-1304. |
| [14] | S. H. JO, D. LEE. Flexural-wave-generation using a phononic crystal with a piezoelectric defect [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(8): 1241-1262. |
| [15] | Haoran BAI, Zhanyu WANG, Sangyu LUO, Zhaoliang QU, Daining FANG. A modified single edge V-notched beam method for evaluating surface fracture toughness of thermal barrier coatings [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(5): 693-710. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS