Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (8): 1511-1532.doi: https://doi.org/10.1007/s10483-025-3281-8
Previous Articles Next Articles
C. C. PARRA1, R. VENEGAS1,†( ), T. G. ZIELIŃSKI2
), T. G. ZIELIŃSKI2
Received:2025-03-10
Revised:2025-06-06
Published:2025-07-28
Contact:
R. VENEGAS, E-mail: rodolfo.venegas@uach.clSupported by:2010 MSC Number:
C. C. PARRA, R. VENEGAS, T. G. ZIELIŃSKI. Acoustic wave propagation in double-porosity permeo-elastic media. Applied Mathematics and Mechanics (English Edition), 2025, 46(8): 1511-1532.

Fig. 1
REV of an l-periodic double-porosity permeo-elastic material, comprising a microporous matrix Ωm and a connected mesoscopic fluid network Ωf. Highly flexible thin elastic solids, denoted by Γ, are clamped onto a perfectly rigid frame Ωs. The solid-fluid interface is Γs, while Γm represents the interface between the pore fluid network and the microporous matrix. These multiscale metamaterials, referred to as Materials A, have a macroscopic characteristic size L (color online)"
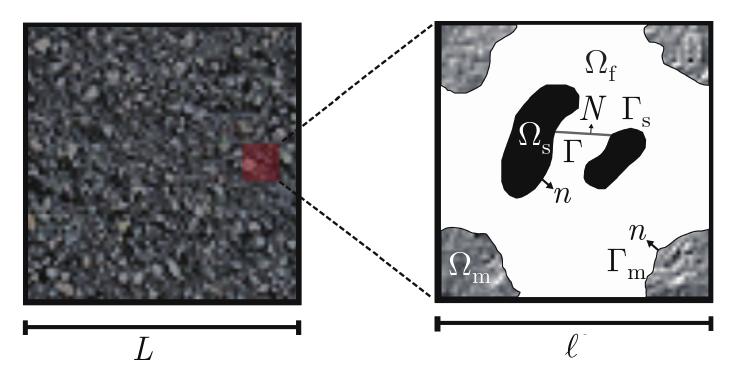

Fig. 4
(a) Real and imaginary parts and (b) normalized phase of the normalized dynamic density ρ(ω)/ρ0 of a multiscale metamaterial of Type A. The vertical dotted and dashed-dotted lines, respectively, correspond to the anti-resonance frequency fa and resonance frequency fg. The dashed lines correspond to the effective parameter of a single-porosity material with the same geometry, but with the films and microporous matrix, respectively, replaced by perfectly rigid and impermeable films and matrix. The x-axis uses a logarithmic scale"
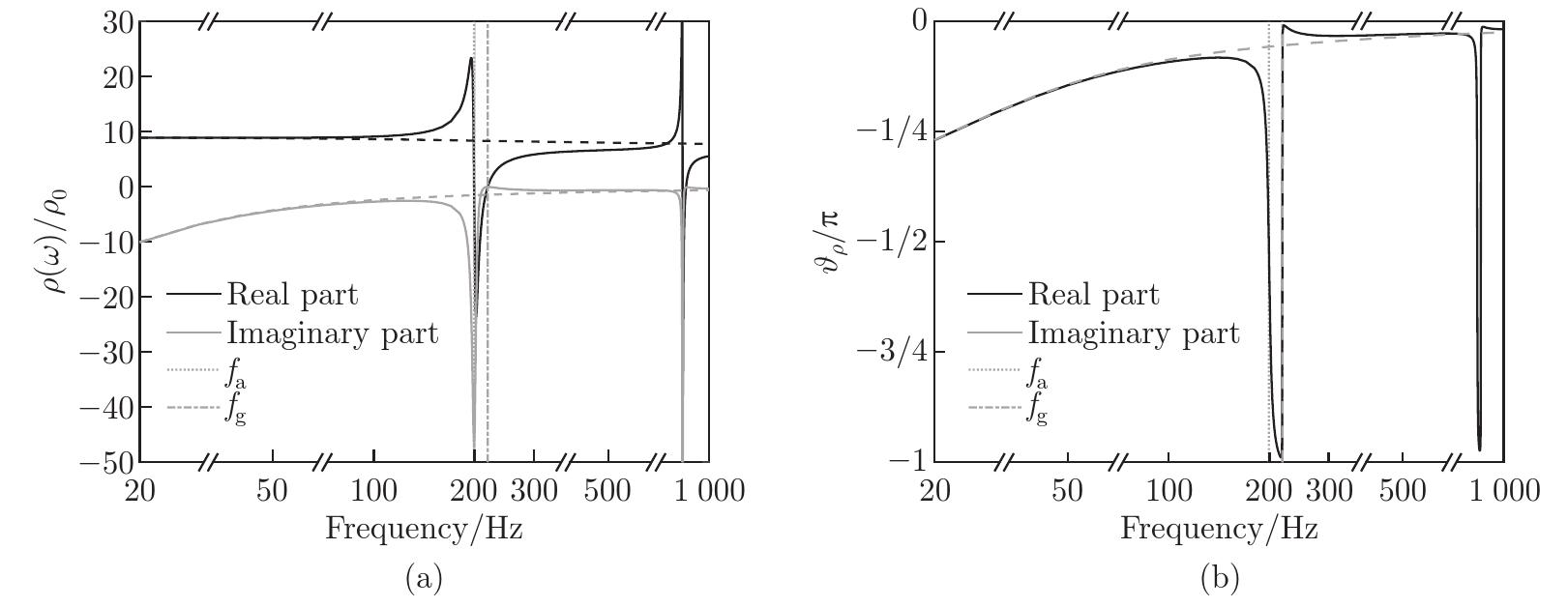
Fig. 5
Real part (continuous lines) and negative of the imaginary (dashed lines) part of the normalized effective compressibility of a multiscale metamaterial of Type A (i.e., P0C), a microporous matrix material P0Cm, and a single-porosity material P0Cp (see the text for its description). The vertical dotted lines correspond to thermal or pressure diffusion characteristic frequencies"
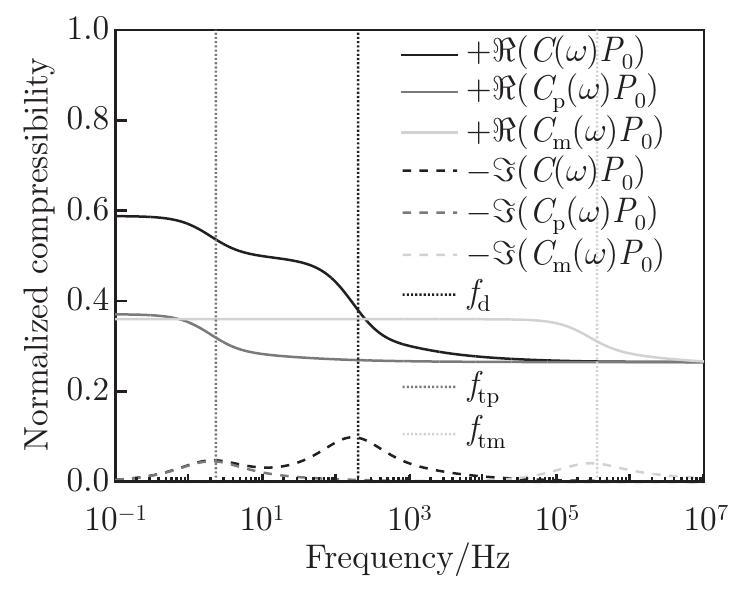

Fig. 6
(a) Magnitude and (b) phase of the effective speed of sound of a multiscale metamaterial of Type A (black lines) and that of a single-porosity material (grey lines) with the same geometry but having the films and microporous matrix replaced by perfectly rigid and impermeable solid materials. The vertical dotted lines correspond to the anti-resonance frequency fa, which is matched to the pressure diffusion characteristic frequency fd, and the resonance frequency fg. The x-axis uses a logarithmic scale"
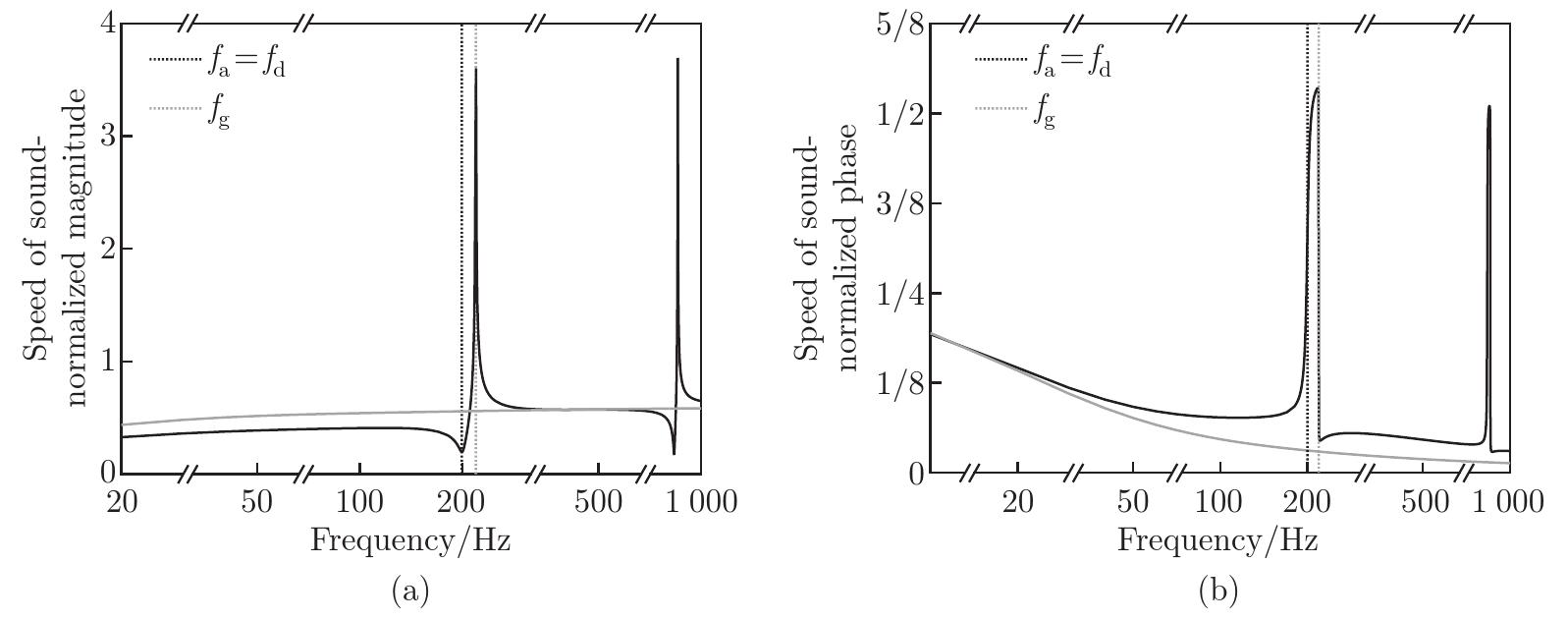

Fig. 7
(a) Normalized magnitude of the effective compressibility (i.e., |CP0|) of a double-porosity permeo-elastic material of Type B and a permeo-elastic material. The plot (b) shows the respective normalized phase of the effective compressibility, i.e., ϑC/π. The vertical dotted lines correspond to the anti-resonance frequency fa′, which is matched to the pressure diffusion characteristic frequency fd, and the resonance frequency fg′. The normalized magnitude |CP0| is bounded from below by |ϕmφmℑ(F(ω))|, as shown by the dashed black line. The x-axis uses a logarithmic scale. DPPE: double-porosity permeo-elastic; PE: permeo-elastic"
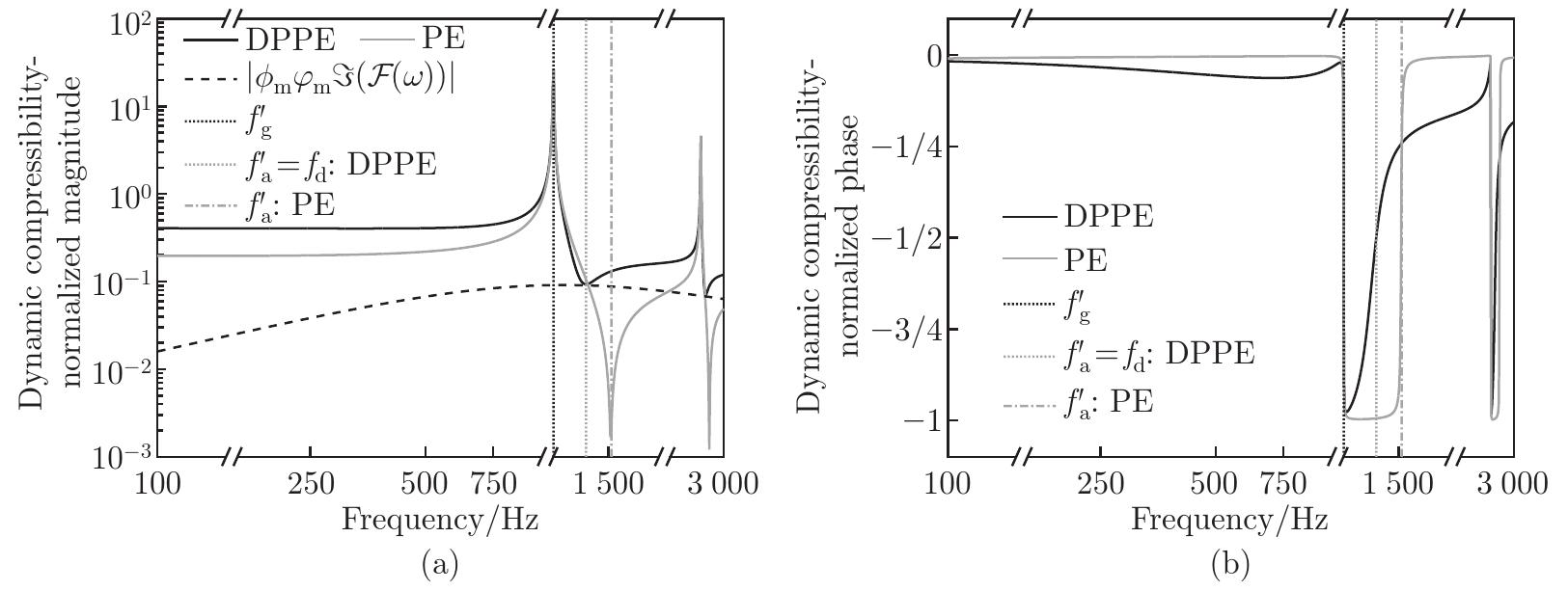
Fig. 8
(a) Normalized magnitude and (b) phase of the effective speed of sound, and (c) normalized phase constant and (d) attenuation coefficient of a double-porosity permeo-elastic material of Type B and a permeo-elastic material. The vertical dotted lines correspond to the anti-resonance frequency fa′, which is matched to the pressure diffusion characteristic frequency fd, and resonance frequency fg′. The dashed black line in plot (a) shows that |c/C0| is bounded from above by ϕp/|α∞γφmϕmℑ(F)|. The x-axis uses a logarithmic scale. DPPE: double-porosity permeo-elastic; PE: permeo-elastic"
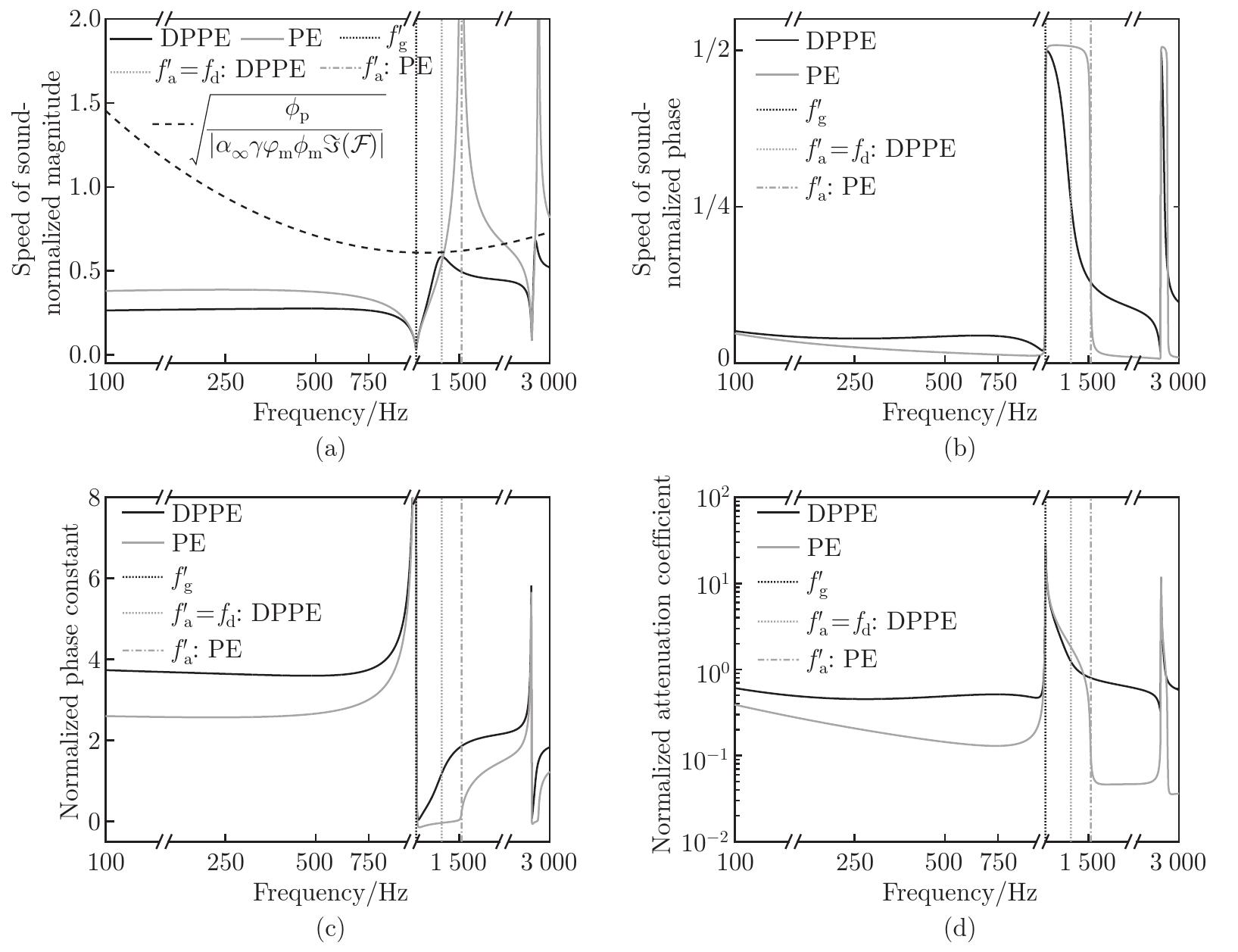
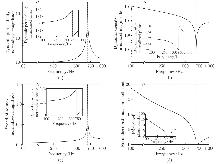
Fig. 9
Normalized magnitudes of (a) dynamic permeability |K(ω)|/(φmKm0) and (b) density |ρ(ω)/ρ0| of a double-porosity permeo-elastic material of Type C. The dashed vertical line represents the resonance frequency ωg, and the inset plots show the normalized phase of the dynamic permeability and density. Normalized (c) magnitude of the effective speed of sound |c(ω)/c0| and (d) attenuation coefficient −ℑ(kc)c0/ω of a double-porosity permeo-elastic material of Type C. The dashed vertical line represents the resonance frequency ωg. The inset plots show the normalized (c) phase of the effective speed of sound and (d) phase constant. The x-axis uses a logarithmic scale"
| [1] | OLNY, X. and BOUTIN, C. Acoustic wave propagation in double porosity media. The Journal of the Acoustical Society of America, 114(1), 73–89 (2003) |
| [2] | VENEGAS, R. and UMNOVA, O. Acoustical properties of double porosity granular materials. The Journal of the Acoustical Society of America, 130(5), 2765–2776 (2011) |
| [3] | VENEGAS, R. and BOUTIN, C. Acoustics of sorptive porous materials. Wave Motion, 68, 162–181 (2017) |
| [4] | VENEGAS, R., BOUTIN, C., and UMNOVA, O. Acoustics of multiscale sorptive porous materials. Physics of Fluids, 29(8), 082006 (2017) |
| [5] | VENEGAS, R. and BOUTIN, C. Acoustics of permeable heterogeneous materials with local non-equilibrium pressure states. Journal of Sound and Vibration, 418, 221–239 (2018) |
| [6] | VENEGAS, R., ZIELIŃSKI, T. G., NÚNEZ, G., and BÉCOT, F. X. Acoustics of porous composites. Composites Part B: Engineering, 220, 109006 (2021) |
| [7] | VENEGAS, R. and BOUTIN, C. Acoustics of permeo-elastic materials. Journal of Fluid Mechanics, 828, 135–174 (2017) |
| [8] | BOUTIN, C. and VENEGAS, R. Pore-scale bending and membrane effects in permeo-elastic media. Mechanics of Materials, 145, 103362 (2020) |
| [9] | BOUTIN, C. and VENEGAS, R. Morphology influence on the acoustic properties of permeo-elastic media. Wave Motion, 115, 103080 (2022) |
| [10] | AURIAULT, J. L., BOUTIN, C., and GEINDREAU, C. Homogenization of Coupled Phenomena in Heterogeneous Media, ISTE Ltd and John Wiley & Sons, London and Hoboken, NJ, 1–473 (2009) |
| [11] | ARENAS, J. P., PARRA, C. C., REBOLLEDO, J., and VENEGAS, R. Granular pumice stone: a natural double-porosity sound-absorbing material. Buildings, 15(4), 557 (2025) |
| [12] | ZIELIŃSKI, T. G., DAUCHEZ, N., BOUTIN, T., LETURIA, M., WILKINSON, A., CHEVILLOTTE, F., BÉCOT, F. X., and VENEGAS, R. Taking advantage of a 3D printing imperfection for the development of sound-absorbing materials. Applied Acoustics, 197, 108941 (2022) |
| [13] | ALLARD, J. F. and ATALLA, N. Propagation of Sound in Porous Media: Modeling Sound Absorbing Materials, 2nd ed., John Wiley & Sons, Hoboken, NJ, 1–358 (2009) |
| [14] | AURIAULT, J. L., BORNE, L., and CHAMBON, R. Dynamics of porous saturated media, checking of the generalized law of Darcy. The Journal of the Acoustical Society of America, 77(5), 1641–1650 (1985) |
| [15] | JOHNSON, D. L., KOPLIK, J., and DASHEN, R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. Journal of Fluid Mechanics, 176, 379–402 (1987) |
| [16] | LAFARGE, D., LEMARINIER, P., ALLARD, J. F., and TARNOW, V. Dynamic compressibility of air in porous structures at audible frequencies. The Journal of the Acoustical Society of America, 102(4), 1995–2006 (1997) |
| [17] | ZIELIŃSKI, T. G., VENEGAS, R., PERROT, C., ČERVENKA, M., CHEVILLOTTE, F., and ATTENBOROUGH, K. Benchmarks for microstructure-based modelling of sound absorbing rigid-frame porous media. Journal of Sound and Vibration, 483, 115441 (2020) |
| [18] | UMNOVA, O., ATTENBOROUGH, K., and LI, K. M. Cell model calculations of dynamic drag parameters in packings of spheres. The Journal of the Acoustical Society of America, 107(6), 3113–3119 (2000) |
| [19] | UMNOVA, O., TSIKLAURI, D., and VENEGAS, R. Effect of boundary slip on the acoustical properties of microfibrous materials. The Journal of the Acoustical Society of America, 126(4), 1850–1861 (2009) |
| [20] | TRINH, V. H., LANGLOIS, V., GUILLEMINOT, J., PERROT, C., KHIDAS, Y., and PITOIS, O. Tuning membrane content of sound absorbing cellular foams: fabrication, experimental evidence and multiscale numerical simulations. Materials and Design, 162, 345–361 (2019) |
| [21] | STINSON, M. R. The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape. The Journal of the Acoustical Society of America, 89(2), 550–558 (1991) |
| [22] | AURIAULT, J. L. and BOUTIN, C. Long wavelength inner-resonance cut-off frequencies in elastic composite materials. International Journal of Solids and Structures, 49(23-24), 3269–3281 (2012) |
| [23] | BOUTIN, C. Acoustics of porous media with inner resonators. The Journal of the Acoustical Society of America, 134(6), 4717–4729 (2013) |
| [24] | VENEGAS, R., NÚNEZ, G., BOUTIN, C., UMNOVA, O., and ZHANG, Q. Acoustic wave propagation in permeable lossy metamaterials. Physics of Fluids, 34(1), 017117 (2022) |
| [25] | ZHANG, J., HU, B., and WANG, S. Review and perspective on acoustic metamaterials: from fundamentals to applications. Applied Physics Letters, 123(1), 010502 (2023) |
| [26] | WANG, K., ZHOU, J., TAN, D., LI, Z., LIN, Q., and XU, D. A brief review of metamaterials for opening low-frequency band gaps. Applied Mathematics and Mechanics (English Edition), 43, 1125–1144 (2022) https://doi.org/10.1007/s10483-022-2870-9 |
| [27] | LIU, J., LI, J., and WU, Y. Bandgap adjustment of a sandwich-like acoustic metamaterial plate with a frequency-displacement feedback control method. Applied Mathematics and Mechanics (English Edition), 45, 1807–1820 (2024) https://doi.org/10.1007/s10483-024-3167-8 |
| [28] | HAN, D., JIA, Q., GAO, Y., JIN, Q., FANG, X., WEN, J., and YU, D. Local resonance metamaterial-based integrated design for suppressing longitudinal and transverse waves in fluid-conveying pipes. Applied Mathematics and Mechanics (English Edition), 45, 1821–1840 (2024) https://doi.org/10.1007/s10483-024-3166-8 |
| [29] | DONG, X., WANG, S., WANG, A., WANG, L., ZHANG, Z., TIE, Y., LIN, Q., and SUN, Y. Low-frequency bandgap and vibration suppression mechanism of a novel square hierarchical honeycomb metamaterial. Applied Mathematics and Mechanics (English Edition), 45, 1841–1856 (2024) https://doi.org/10.1007/s10483-024-3168-7 |
| [30] | WANG, S., WANG, A., WU, Y., LI, X., SUN, Y., ZHANG, Z., DING, Q., AYALEW, G. D., MA, Y., and LIN, Q. Ultra-wide band gap and wave attenuation mechanism of a novel star-shaped chiral metamaterial. Applied Mathematics and Mechanics (English Edition), 45, 1261–1278 (2024) https://doi.org/10.1007/s10483-024-3156-8 |
| [31] | JIA, Q., YU, D., HAN, D., and WEN, J. Lightweight multifunctional metamaterial with low-frequency vibroacoustic reduction and load-bearing performances. Applied Mathematics and Mechanics (English Edition), 46, 403–422 (2025) https://doi.org/10.1007/s10483-025-3231-6 |
| [32] | LIU, Z., ZHANG, X., MAO, Y., ZHU, Y. Y., YANG, Z., CHAN, C. T., and SHENG, P. Locally resonant sonic materials. Science, 289(5485), 1734–1736 (2000) |
| [33] | FANG, N., XI, D., XU, J., AMBATI, M., SRITURAVANICH, W., SUN, C., and ZHANG, X. Ultrasonic metamaterials with negative modulus. Nature Materials, 5, 452–456 (2006) |
| [34] | KRYNKIN, A., UMNOVA, O., BOON CHONG, A. Y., TAHERZADEH, S., and ATTENBOROUGH, K. Predictions and measurements of sound transmission through a periodic array of elastic shells in air. The Journal of the Acoustical Society of America, 128(6), 3496–3506 (2010) |
| [35] | YANG, Z., MEI, J., YANG, M., CHAN, N. H., and SHENG, P. Membrane-type acoustic metamaterial with negative dynamic mass. Physical Review Letters, 101(20), 204301 (2008) |
| [36] | GAULON, C., PIERRE, J., DEREC, C., JAOUEN, L., BÉCOT, F. X., CHEVILLOTTE, F., ELIAS, F., DRENCKHAN, W., and LEROY, V. Acoustic absorption of solid foams with thin membranes. Applied Physics Letters, 112(26), 261904 (2018) |
| [37] | BONGARD, F., LISSEK, H., and MOSIG, J. R. Acoustic transmission line metamaterial with negative/zero/positive refractive index. Physical Review B, 82(9), 094306 (2010) |
| [38] | SEO, Y. M., PARK, J. J., LEE, S. H., PARK, C. M., KIM, C. K., and LEE, S. H. Acoustic metamaterial exhibiting four different sign combinations of density and modulus. Journal of Applied Physics, 111(2), 023504 (2012) |
| [39] | QUE, W., YANG, X., and ZHANG, W. Tunable low frequency band gaps and sound transmission loss of a lever-type metamaterial plate. Applied Mathematics and Mechanics (English Edition), 43, 1145–1158 (2022) https://doi.org/10.1007/s10483-022-2890-9 |
| [40] | ARENAS, J. P., MARIN, V., and VENEGAS, R. Membrane sound absorber with a granular activated carbon infill. Applied Acoustics, 202, 109180 (2023) |
| [41] | ZHAO, H., WANG, Y., YU, D., YANG, H., ZHONG, J., WU, F., and WEN, J. A double porosity material for low frequency sound absorption. Composite Structures, 239, 111978 (2020) |
| [42] | ZHANG, W., LIU, X., and XIN, F. Normal incidence sound absorption of an acoustic labyrinthine metal-fibers-based porous metamaterial at high temperature. International Journal of Mechanical Sciences, 237, 107821 (2023) |
| [43] | LI, Y., YAN, J., and PENG, Y. Multiscale porous with coiled-up channel for low-frequency broadband sound absorption. International Journal of Mechanical Sciences, 232, 107622 (2022) |
| [44] | GAO, N., TANG, L., DENG, J., LU, K., HOU, H., and CHEN, K. Design, fabrication and sound absorption test of composite porous metamaterial with embedding I-plates into porous polyurethane sponge. Applied Acoustics, 175, 107845 (2021) |
| [45] | WANG, S., XIAO, Y., GU, J., HU, C., ZHANG, H., and WEN, J. Double-panel metastructure lined with porous material for broadband low-frequency sound insulation. Applied Acoustics, 207, 109332 (2023) |
| [1] | Haidong LIN, Yiqi MAO, Shujuan HOU. Homogenization-based numerical framework of second-phase reinforced alloys integrating strain gradient effects [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(7): 1273-1294. |
| [2] | Youjiang CUI, Zhihui XU, Que ZHOU, Baolin WANG, Kaifa WANG, Biao WANG. Effective elastic modulus and energy absorption performance evaluations of a novel re-entrant chiral hybrid honeycomb [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 781-794. |
| [3] | Qi JIA, Dianlong YU, Donghai HAN, Jihong WEN. Lightweight multifunctional metamaterial with low-frequency vibroacoustic reduction and load-bearing performances [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(3): 403-422. |
| [4] | Shuai MO, Xu TANG, Keren CHEN, H. HOUJOH, Wei ZHANG. Continuously adjustable mechanical metamaterial based on planetary gear trains and external meshing gears [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(2): 233-252. |
| [5] | Fan YANG, Zhaoyang MA, Xingming GUO. Bandgap characteristics analysis and graded design of a novel metamaterial for flexural wave suppression [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(1): 1-24. |
| [6] | Wei CHEN, Zhihong TANG, Yufen LIAO, Linxin PENG. A six-variable quasi-3D isogeometric approach for free vibration of functionally graded graphene origami-enabled auxeticmetamaterial plates submerged in a fluid medium [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(1): 157-176. |
| [7] | Jinlian REN, Peirong LU, Tao JIANG, Jianfeng LIU, Weigang LU. A flexible multiscale algorithm based on an improved smoothed particle hydrodynamics method for complex viscoelastic flows [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(8): 1387-1402. |
| [8] | Shuo WANG, Anshuai WANG, Yansen WU, Xiaofeng LI, Yongtao SUN, Zhaozhan ZHANG, Qian DING, G. D. AYALEW, Yunxiang MA, Qingyu LIN. Ultra-wide band gap and wave attenuation mechanism of a novel star-shaped chiral metamaterial [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1261-1278. |
| [9] | Long ZHAO, Zeqi LU, Hu DING, Liqun CHEN. A viscoelastic metamaterial beam for integrated vibration isolation and energy harvesting [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1243-1260. |
| [10] | Zhou HU, Zhibo WEI, Yan CHEN, Rui ZHU. Reconfigurable mechanism-based metamaterials for ternary-coded elastic wave polarizers and programmable refraction control [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1225-1242. |
| [11] | Xingzhong WANG, Shiteng RUI, Shaokun YANG, Weiquan ZHANG, Fuyin MA. A low-frequency pure metal metamaterial absorber with continuously tunable stiffness [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1209-1224. |
| [12] | Wei WEI, Feng GUAN, Xin FANG. A low-frequency and broadband wave-insulating vibration isolator based on plate-shaped metastructures [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1171-1188. |
| [13] | Changqi CAI, Chenjie ZHU, Fengyi ZHANG, Jiaojiao SUN, Kai WANG, Bo YAN, Jiaxi ZHOU. Modeling and analysis of gradient metamaterials for broad fusion bandgaps [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1155-1170. |
| [14] | Yuxin YAO, Yuansheng MA, Fang HONG, Kai ZHANG, Tingting WANG, Haijun PENG, Zichen DENG. On Klein tunneling of low-frequency elastic waves in hexagonal topological plates [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1139-1154. |
| [15] | Chao WANG, Honggang ZHAO, Yang WANG, Jie ZHONG, Dianlong YU, Jihong WEN. Topology optimization of chiral metamaterials with application to underwater sound insulation [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1119-1138. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS