Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (11): 2055-2074.doi: https://doi.org/10.1007/s10483-025-3311-6
Previous Articles Next Articles
Xingchi CAO, Xin FANG†( ), Dianlong YU
), Dianlong YU
Received:2025-07-04
Revised:2025-09-02
Published:2025-10-29
Contact:
†Xin FANG, E-mail: xinfangdr@sina.comSupported by:2010 MSC Number:
Xingchi CAO, Xin FANG, Dianlong YU. Stiffness gradient sensitivity analysis method for evaluating the vibration reduction effect of complex variable-stiffness systems. Applied Mathematics and Mechanics (English Edition), 2025, 46(11): 2055-2074.
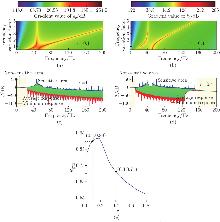
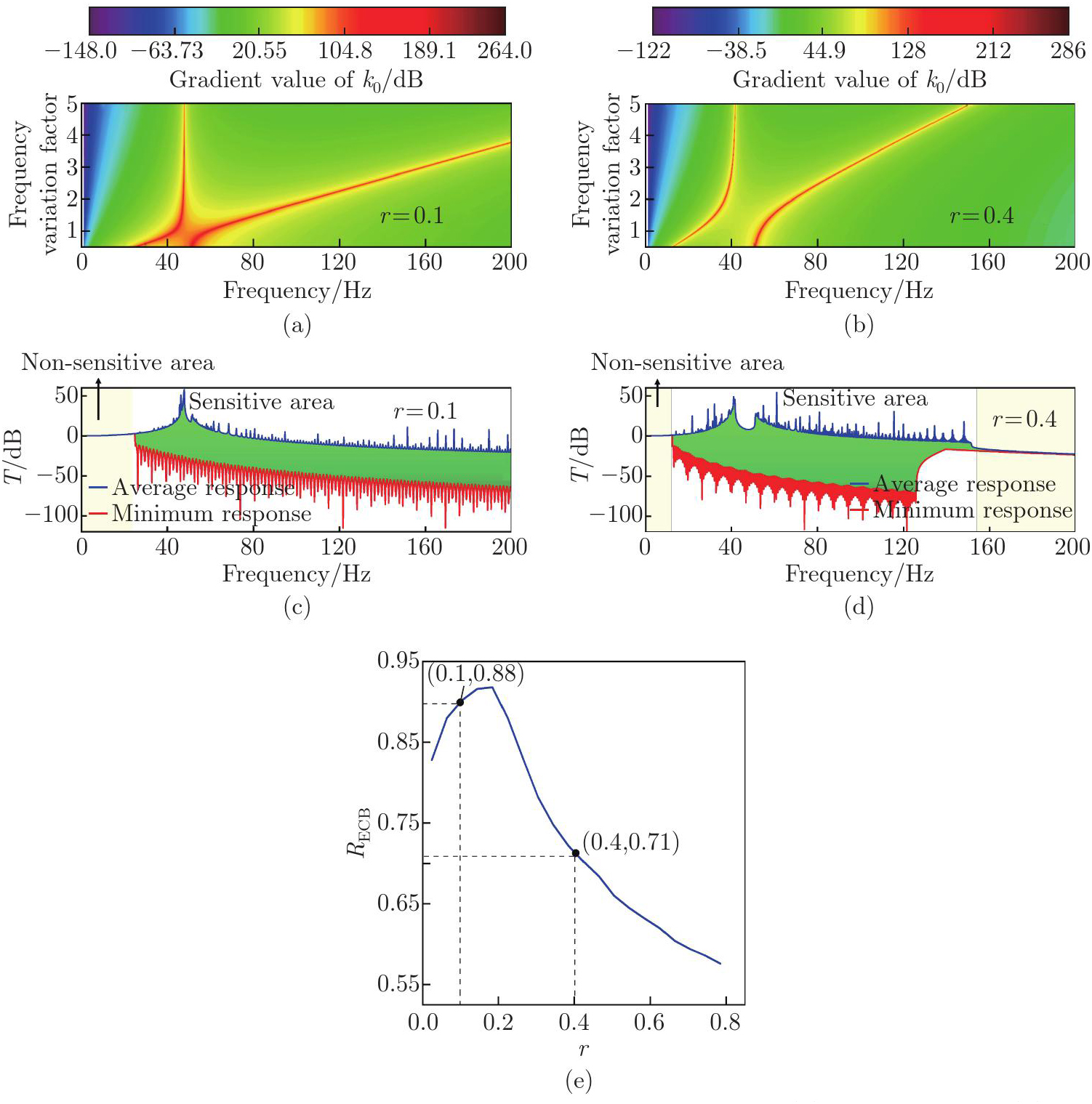
Fig.?3
Global normalized gradient value distributions of k0 when (a) r=0.1 and (b) r=0.4. Minimum and average responses at each frequency point via k0 tuning when (c) r=0.1 and (d) r=0.4, where the shade of color represents the value of the normalized gradient. (e) Variation of RECB with r (color online)"
Table?1
Natural frequencies and frequency variation ranges of the 12 subsystems"
| Subsystem | Natural frequency/Hz | Frequency variation range/Hz |
|---|---|---|
| 11 | 400 | [200, 2 000] |
| 12 | 66.7 | [33, 333] |
| 13 | 115.5 | [57.7, 577] |
| 21 | 400 | [200, 2 000] |
| 22 | 70.7 | [35.4, 354] |
| 23 | 89.4 | [44.7, 447] |
| 31 | 400 | [200, 2 000] |
| 32 | 66.7 | [33.3, 333] |
| 33 | 141.4 | [70.7, 707] |
| 41 | 400 | [200, 2 000] |
| 42 | 57.7 | [28.9, 289] |
| 43 | 81.6 | [40.8, 408] |
Table?2
Five sets of mass ratios for the 12 subsystems"
| Subsystem | Initial mass | Random mass 1 | Random mass 2 | Random mass 3 | Random mass 4 |
|---|---|---|---|---|---|
| 11 | 0.002 3 | 0.035 4 | 0.093 4 | 0.043 0 | 0.033 0 |
| 12 | 0.082 6 | 0.088 6 | 0.024 4 | 0.073 5 | 0.011 2 |
| 13 | 0.027 5 | 0.068 4 | 0.021 1 | 0.019 2 | 0.073 0 |
| 21 | 0.002 3 | 0.056 1 | 0.021 3 | 0.048 4 | 0.047 3 |
| 22 | 0.073 4 | 0.015 1 | 0.034 7 | 0.055 6 | 0.013 7 |
| 23 | 0.045 9 | 0.015 1 | 0.059 1 | 0.005 1 | 0.053 1 |
| 31 | 0.002 3 | 0.006 1 | 0.048 9 | 0.057 0 | 0.004 4 |
| 32 | 0.082 6 | 0.080 8 | 0.033 2 | 0.016 6 | 0.096 9 |
| 33 | 0.018 3 | 0.056 2 | 0.068 8 | 0.006 8 | 0.028 2 |
| 41 | 0.002 3 | 0.066 2 | 0.016 4 | 0.088 7 | 0.070 8 |
| 42 | 0.110 1 | 0.002 6 | 0.033 3 | 0.090 3 | 0.033 8 |
| 43 | 0.055 0 | 0.090 4 | 0.041 6 | 0.075 6 | 0.055 8 |
| [13] | LI, Y. L. and XU, D. L. Vibration attenuation of high dimensional quasi-zero stiffness floating raft system. International Journal of Mechanical Sciences, 126, 186–195 (2017) |
| [14] | ZHAN, Q. C., CHEN, Y. L., ZHAO, Y. H., CHEN, M. F., and GUO, R. S. Vibration suppressing study of a simplified floating raft system by mixing using a nonlinear connecting intercalary plate and connecting nonlinear oscillators. Thin-Walled Structures, 206, 112686 (2025) |
| [15] | WANG, X. Z., RUI, S. T., YANG, S. K., ZHANG, W. Q., and MA, F. Y. A low-frequency pure metal metamaterial absorber with continuously tunable stiffness. Applied Mathematics and Mechanics (English Edition), 45(7), 1209–1224 (2024) https://doi.org/10.1007/s10483-024-3158-7 |
| [16] | SUN, X. T., XU, J., and QI, Z. F. Mechanism properties of a bird-neck bionic rigid-flexible structure. Fundamental Research, 4(6), 1613–1624 (2024) |
| [17] | XIAO, C. D., TIAN, R. L., ZHANG, X. L., and LI, S. Variable stiffness and zero Poisson’s ratio of the butterfly-shaped mechanical metamaterial. Composites Communications, 49, 101958 (2024) |
| [18] | PAGLIARANI, N., ARLEO, L., DE LUCA, G., POZZI, J., and CIANCHETTI, M. Variable stiffness structure inspired by seashells. Smart Materials and Structures, 33(2), 025004 (2024) |
| [19] | HU, T., JIANG, L., PAN, L. Y., CHEN, B., GONG, N., YANG, J., GONG, X. L., and SUN, S. S. Development of a semi-active suspension using a compact magnetorheological damper with negative-stiffness components. Mechanical Systems and Signal Processing, 223, 111842 (2025) |
| [20] | XU, L. H., XIE, X. S., and LI, Z. X. Seismic performance and resilience of composite damping self-centering braced frame structures. Fundamental Research, 4(3), 603–610 (2024) |
| [21] | NABIL, T., BAKR, M., EL-DOMIATY, A., DAWOOD, M., and MANSOUR, T. M. Vibration damping by enhancing of magneto-rheological damper performance using novel smart fluid. Mechanics Based Design of Structures and Machines, 53(2), 1351–1367 (2025) |
| [22] | DEMIR, M. U. and YILMAZ, C. Realization of a wideband three-axis horizontal vibration isolator with adjustable stiffness and damping. Journal of Sound and Vibration, 600, 118876 (2025) |
| [23] | TIAN, R. L., WANG, M. H., ZHANG, Y. S., JING, X. J., and ZHANG, X. L. A concave X-shaped structure supported by variable pitch springs for low-frequency vibration isolation. Mechanical Systems and Signal Processing, 218, 111587 (2024) |
| [24] | CHAI, Z. Y., HAN, J. T., SONG, X. Y., ZANG, J., ZHANG, Y. W., and ZHANG, Z. Theoretical and experimental investigations on an X-shaped vibration isolator with active controlled variable stiffness. Applied Mathematics and Mechanics (English Edition), 45(8), 1371–1386 (2024) https://doi.org/10.1007/s10483-024-3135-6 |
| [25] | FANG, X., WEN, J. H., CHENG, L., YU, D. L., ZHANG, H. J., and GUMBSCH, P. Programmable gear-based mechanical metamaterials. Nature Materials, 21(8), 869–876 (2022) |
| [26] | FANG, X., WEN, J., YU, D., GUMBSCH, P., and GAO, H. Gear-based metamaterials for extraordinary bandgap tunability. Applied Physics Letters, 127(11), 112201 (2025) |
| [27] | LIN, Y., WEN, G. L., LIU, C. X., HE, J. F., and LIU, J. A magnetorheological elastomer-based hybrid vibration isolation system with semi-active control and quasi-zero stiffness performance. International Journal of Non-Linear Mechanics, 174, 105063 (2025) |
| [28] | LI, Z. Y., WANG, K., CHEN, T. T., CHENG, L., XU, D. L., and ZHOU, J. X. Temperature controlled quasi-zero-stiffness metamaterial beam for broad-range low-frequency band tuning. International Journal of Mechanical Sciences, 259, 108593 (2023) |
| [29] | WEN, G. L., ZHANG, S. D., WANG, H. X., WANG, Z. P., HE, J. F., CHEN, Z. J., LIU, J., and XIE, Y. M. Origami-based acoustic metamaterial for tunable and broadband sound attenuation. International Journal of Mechanical Sciences, 239, 107872 (2023) |
| [30] | SONG, J., WANG, B. F., and HAO, X. H. Optimization algorithms and their applications and prospects in manufacturing engineering. Materials, 17(16), 4093 (2024) |
| [31] | MENG, X. L. An automatic frequency control system for transmission machinery based on back-propagation neural network algorithm in the Internet of Things environment. Journal of Testing and Evaluation, 52(3), 1376–1388 (2024) |
| [32] | ZHANG, T. S., YE, M., LI, X. F., BI, D. J., PENG, L. B., and XIE, Y. L. Fractional derivative kernel recursive generalized maximum correntropy for RUL prediction of rolling bearings. Mechanical Systems and Signal Processing, 217, 111527 (2024) |
| [33] | GONDZIO, J. and SOBRAL, F. N. C. Polynomial worst-case iteration complexity of quasi-Newton primal-dual interior point algorithms for linear programming. Computational Optimization and Applications, 91(2), 649–681 (2024) |
| [34] | LIU, Q., YU, Y. C., HAN, B. S., and ZHOU, W. A novel compact high-sensitivity fiber Bragg grating sensor for microvibration measurement of robot joints. IEEE Sensors Journal, 24(8), 12385–12399 (2024) |
| [35] | HASHEMIAN, F., YANG, H. Z., WANG, Y., DENG, X. M., KIM, S., and VAIDHYANATHAN, R. Parametric dynamic simulation and Bayesian design optimization of a front-loading washing machine. Journal of Vibration Engineering & Technologies, 12(1), 41–62 (2024) |
| [36] | KAMGAR, R., RAHMANI, F., and RAHGOZAR, R. Geometrical and material optimization of the functionally graded doubly-curved shell by metaheuristic optimization algorithms. Structures, 62, 106254 (2024) |
| [37] | ZHU, H. X., LI, S., ZHU, R. Y., GAO, F. Y., YIN, Z. Y., LIU, L. Q., and ZHENG, X. F. Residual vibration suppression of piezoelectric inkjet printing based on particle swarm optimization algorithm. Micromachines, 15(10), 1192 (2024) |
| [38] | XU, H. T., GAO, J., WEN, J. N., DU, J. S., and WANG, W. Data-driven simulation of aero-engine rotor assembly process optimization for unbalance based on fusion algorithm. Aerospace Science and Technology, 158, 109874 (2025) |
| [39] | QIU, Z. C., and LIU, Y. H. Visual feedback vibration control of flexible hinged plate system based on reinforcement learning algorithm. Mechanical Systems and Signal Processing, 224, 112005 (2025) |
| [40] | YIN, G. H., MA, M. L., JIA, P., and MA, X. X. Parameter optimization of friction pendulum bearings based on the adaptive genetic algorithm considering the overall evolutionary status. Buildings, 14(2), 435 (2024) |
| [41] | GUO, Y., XU, G. F., and DUAN, C. Y. Research on time-delayed vibration reduction control of 1/4 vehicle semi-active suspension system with three degrees of freedom. Advances in Mechanical Engineering, 16(9), 16878132241273541 (2024) |
| [42] | LIU, G., PAN, L., JIANG, W. Q., FAN, S., and BUHARI, A. Dynamic performance and optimization research for six-link mechanism considering the coupling effect of flexible structure and wear clearances. Nonlinear Dynamics, 112(6), 4299–4320 (2024) |
| [43] | LIN, Q., HU, J. X., ZHOU, Q., SHU, L. S., and ZHANG, A. F. A multi-fidelity Bayesian optimization approach for constrained multi-objective optimization problems. Journal of Mechanical Design, 146(7), 071702 (2024) |
| [1] | CHENG, J. W., BU, W. J., SHI, L., and FU, J. Q. A real-time shaft alignment monitoring method adapting to ship hull deformation for marine propulsion system. Mechanical Systems and Signal Processing, 197, 110366 (2023) |
| [2] | ZHANG, Y. T., SHEN, W. A., LONG, Z. T., ZHANG, Y. P., WANG, Z. C., ZHANG, Z. K., ZHU, S. Y., STOCCHINO, A., DENG, H. X., and ZHU, H. P. Active pendulation control of hoisting systems of ship-mounted cranes under ocean wave excitations: principle and experimental study. Mechanical Systems and Signal Processing, 222, 111802 (2025) |
| [3] | SHARMA, S. K., SHARMA, R. C., and LEE, J. Propelling precision of longitudinal vibration mitigation in ship propeller shafts through advanced nonlinear intelligent semi-active control leveraging adaptive neuro-fuzzy inference system with linear quadratic regulator. Journal of Vibration and Control, 31(7-8), 1472–1484 (2025) |
| [4] | WU, Y. W., DAI, Q. H., LIU, H. F., TANG, Y., and CHEN, X. C. Ship base vibration reduction design technology based on visualization of power flow and discrete optimization. Ocean Engineering, 309, 118494 (2024) |
| [5] | DAI, S. J., LIU, S. Y., JI, W. B., and LI, S. D. Vibration suppression in macro-micro grinding system of aeroengine blade based on impedance compensation prediction control strategy. The International Journal of Advanced Manufacturing Technology, 125(1), 793–807 (2023) |
| [6] | HU, B., FANG, X., WEN, J. H., and YU, D. L. Effectively reduce transient vibration of 2D wing with bi-stable metamaterial. International Journal of Mechanical Sciences, 272, 109172 (2024) |
| [7] | LAGEMANN, E., BRUNTON, S. L., SCHRÖEDER, W., and LAGEMANN, C. Towards extending the aircraft flight envelope by mitigating transonic airfoil buffet. Nature Communications, 15, 5020 (2024) |
| [8] | VAN DER VEEK, B., GUTIERREZ, H., WISE, B., KIRK, D., and VAN BARSCHOT, L. Vibration control of flexible launch vehicles using fiber Bragg grating sensor arrays. Sensors, 25(1), 204 (2025) |
| [9] | ZHOU, X., TONG, W. H., DAI, L., and WEI, B. Y. Vibration isolation and launch performance enhancement of the spacecraft in-orbit launch design using the nonlinear dynamic feature. Applied Sciences, 14(10), 4250 (2024) |
| [10] | KONG, C. Y., ZHAO, D. J., and LIANG, B. G. Vibration suppression of a flexible beam structure coupled with liquid sloshing via ADP control based on FBG strain measurement. Actuators, 12(12), 471 (2023) |
| [11] | SHENG, P., HU, B., FANG, X., and WEN, J. H. Random aeroelastic vibration of nonlinear metamaterial supersonic plates. International Journal of Mechanical Sciences, 297-298, 110371 (2025) |
| [44] | ORTIZ, R., MIRANDA-CHIQUITO, P., ENCALADA-DAVILA, A., MARQUEZ, L. E., TUTIVEN, C., CHATZI, E., and SILVA, C. E. An enhanced modeling framework for bearing fault simulation and machine learning-based identification with Bayesian-optimized hyperparameter tuning. Journal of Computing and Information Science in Engineering, 24(9), 091002 (2024) |
| [45] | WANG, X. G., MING, M. A., ZHAO, B., ZHANG, W. H., and SONG, S. Response surface model optimization algorithm for structural assessment based on vibration frequency. Shock and Vibration, 2025(1), 5446251 (2025) |
| [46] | MA, J. J., LIU, Z. T., WANG, C. S., GUO, Y., LIU, C. L., HAN, Y. W., and WANG, L. H. Multi-objective optimization research on nonlinear energy sink system of finite-length beam on elastic medium. Nonlinear Dynamics, 113(2), 1007–1024 (2025) |
| [47] | WU, Q. B., HE, J. J., CHEN, W. J., LI, Q. H., and LIU, S. T. Topology optimization of phononic crystal with prescribed band gaps. Computer Methods in Applied Mechanics and Engineering, 412, 116071 (2023) |
| [48] | ZHANG, H., DING, X. H., NI, W. Y., CHEN, Y. Y., ZHANG, X. P., and LI, H. Concurrent topology optimization of composite plates for minimum dynamic compliance. Materials, 15(2), 538 (2022) |
| [49] | ZHANG, H., TAKEZAWA, A., DING, X. H., GUO, H. H., NI, W. Y., and ZHANG, X. P. Topology optimization of composite macrostructures comprising multi-phase viscoelastic composite microstructures for enhanced structural damping. Composite Structures, 278, 114712 (2021) |
| [50] | HADIZADEH-BAZAZ, M., NAVARRO, I. J., and YEPES, V. Life-cycle cost assessment using the power spectral density function in a coastal concrete bridge. Journal of Marine Science and Engineering, 11(2), 433 (2023) |
| [51] | DURMAZGEZER, E., YUCEL, U., and OZCELIK, O. Damage identification of a reinforced concrete frame at increasing damage levels by sensitivity-based finite element model updating. Bulletin of Earthquake Engineering, 17(11), 6041–6060 (2019) |
| [52] | ZHAO, R. C., JIAO, Y. H., and QU, X. Q. Scaling design strategy for experimental rotor systems subjected to restricted support stiffness. Applied Mathematical Modelling, 109, 265–282 (2022) |
| [53] | WANG, X., LI, X., YUE, Z. S., YU, R. P., ZHANG, Q. C., DU, S. F., YANG, Z. K., HAN, B., and LU, T. J. Optimal design of metallic corrugated sandwich panels with polyurea-metal laminate face sheets for simultaneous vibration attenuation and structural stiffness. Composite Structures, 256, 112994 (2021) |
| [12] | LI, B. Y., SHUAI, C. G., and MA, J. G. Rolling stability analysis of high-static-low-dynamic stiffness floating raft vibration isolation systems. Journal of Vibration and Control, 29(21-22), 5161–5169 (2023) |
| [54] | VAN DEN WYNGAERT, J. C. E., SCHEVENELS, M., and REYNDERS, E. P. B. Broadband acoustic shape optimization of studs in double-leaf walls. Journal of Sound and Vibration, 485, 115562 (2020) |
| [55] | LEE, D. H., HWANG, W. S., and KIM, C. M. Design sensitivity analysis and optimization of an engine mount system using an FRF-based substructuring method. Journal of Sound and Vibration, 255(2), 383–397 (2002) |
| [56] | JUNG, J., HYUN, J., GOO, S., and WANG, S. An efficient design sensitivity analysis using element energies for topology optimization of a frequency response problem. Computer Methods in Applied Mechanics and Engineering, 296, 196–210 (2015) |
| [57] | GONI, S. A., MONDAL, S., and CHAKRABORTY, S. A new gradient based step size controlled inverse eigen sensitivity algorithm for identification of material and boundary parameters of plates. Journal of Vibration and Control, 23(16), 2619–2634 (2017) |
| [1] | Qi JIA, Dianlong YU, Donghai HAN, Jihong WEN. Lightweight multifunctional metamaterial with low-frequency vibroacoustic reduction and load-bearing performances [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(3): 403-422. |
| [2] | H. ASGHARI, L. MILLER, R. PENTA, J. MERODIO. On an isotropic porous solid cylinder: the analytical solution and sensitivity analysis of the pressure [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(9): 1499-1522. |
| [3] | Changqi CAI, Chenjie ZHU, Fengyi ZHANG, Jiaojiao SUN, Kai WANG, Bo YAN, Jiaxi ZHOU. Modeling and analysis of gradient metamaterials for broad fusion bandgaps [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1155-1170. |
| [4] | Donghai HAN, Qi JIA, Yuanyu GAO, Qiduo JIN, Xin FANG, Jihong WEN, Dianlong YU. Local resonance metamaterial-based integrated design for suppressing longitudinal and transverse waves in fluid-conveying pipes [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1821-1840. |
| [5] | Peng SHENG, Xin FANG, Dianlong YU, Jihong WEN. Nonlinear metamaterial enabled aeroelastic vibration reduction of a supersonic cantilever wing plate [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1749-1772. |
| [6] | H. ASGHARI, H. TOPOL, B. MARKERT, J. MERODIO. Application of the extended Fourier amplitude sensitivity testing (FAST) method to inflated, axial stretched, and residually stressed cylinders [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(12): 2139-2162. |
| [7] | Jihou YANG, Weixing ZHANG, Xiaodong YANG. Integrated device for multiscale series vibration reduction and energy harvesting [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(12): 2227-2242. |
| [8] | Weixing ZHANG, Wei ZHANG, Xiangying GUO. Vertical vibration control using nonlinear energy sink with inertial amplifier [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(10): 1721-1738. |
| [9] | Dongxu DU, Jun YANG, Wei SUN, Hongwei MA, Kunpeng XU. The semi-analytical modeling and vibration reduction analysis of the cylindrical shell with piezoelectric shunt damping patches [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(10): 1675-1700. |
| [10] | Wenhai ZHOU, Youhe ZHOU. Electric-magnetic-force characteristics of rare earth barium copper oxide superconductor high-field coils based on screening effect and strain sensitivity [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(8): 1249-1268. |
| [11] | Meng YANG, Xingjiu LUO, Xiaoqiang ZHANG, Hu DING, Liqun CHEN. Enhancing suspension vibration reduction by diagonal inerter [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(10): 1531-1542. |
| [12] | K. THRIVENI, B. MAHANTHESH. Heat transport of hybrid nanomaterial in an annulus with quadratic Boussinesq approximation [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(6): 885-900. |
| [13] | B. MAHANTHESH, K. THRIVENI. Nanoparticle aggregation effects on radiative heat transport of nanoliquid over a vertical cylinder with sensitivity analysis [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(3): 331-346. |
| [14] | J. MACKOLIL, B. MAHANTHESH. Optimization of heat transfer in the thermal Marangoni convective flow of a hybrid nanomaterial with sensitivity analysis [J]. Applied Mathematics and Mechanics (English Edition), 2021, 42(11): 1663-1674. |
| [15] | Yimin WEI, Sha WEI, Qianlong ZHANG, Xinjian DONG, Zhike PENG, Wenming ZHANG. Targeted energy transfer of a parallel nonlinear energy sink [J]. Applied Mathematics and Mechanics (English Edition), 2019, 40(5): 621-630. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS