Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (11): 2155-2176.doi: https://doi.org/10.1007/s10483-025-3310-9
Previous Articles Next Articles
Yongqi LIU1, Jianwei WANG2, Dong DU2, Guohua NIE1,†( )
)
Received:2025-05-17
Revised:2025-09-03
Published:2025-10-29
Contact:
†Guohua NIE, E-mail: ghnie@tongji.edu.cnSupported by:2010 MSC Number:
Yongqi LIU, Jianwei WANG, Dong DU, Guohua NIE. A variational differential quadrature formulation for buckling analysis of anisogrid composite lattice conical shells. Applied Mathematics and Mechanics (English Edition), 2025, 46(11): 2155-2176.
Table?4
Comparison of VDQ-predicted buckling loads with FE results"
| 16.47 | |||
| 24.40 | |||
| 32.01 | |||
| 37.83 | |||
| 44.73 | |||
| * | |||
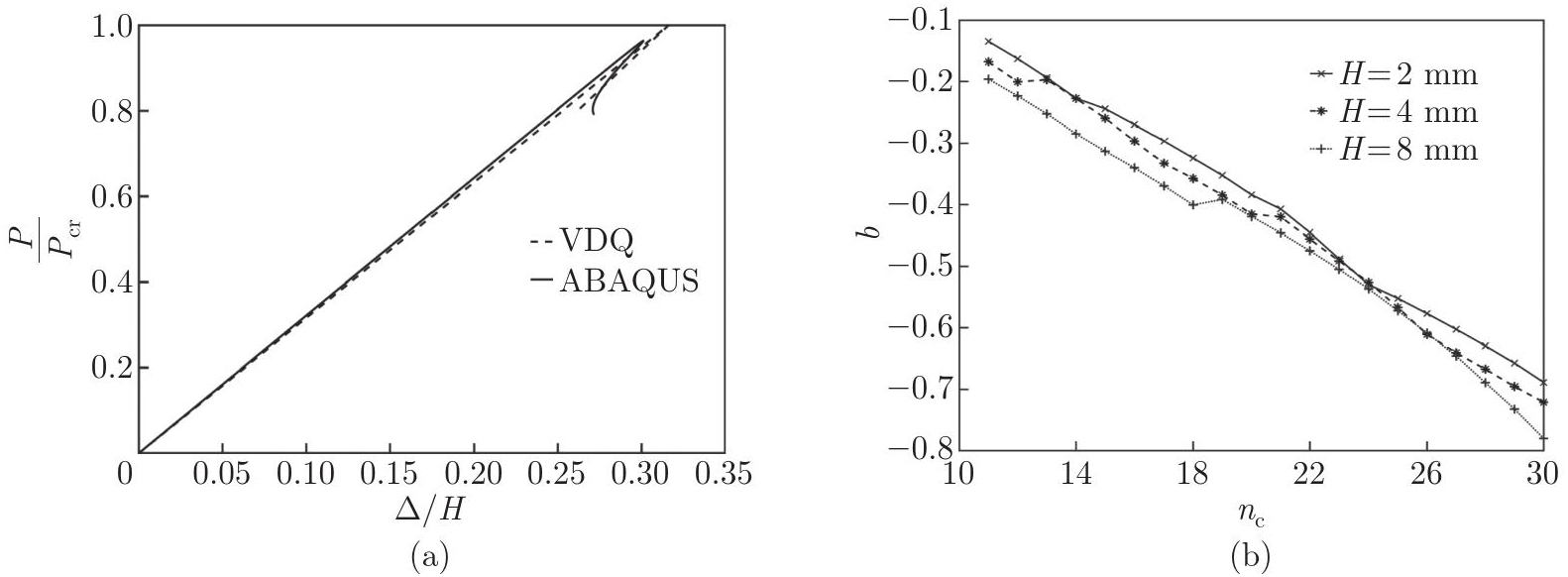
Fig.?11
(a) Comparison of equilibrium paths for a composite lattice conical shell in the initial post-buckling range, where Pcr is the critical buckling load calculated by the VDQ method. (b) Effect of the rib layout and cross-sectional geometry on the b-imperfection sensitivity parameter (color online)"
| [1] | VASILIEV, V. V., BARYNIN, V. A., and RASIN, A. F. Anisogrid lattice structures — survey of development and application. Composite Structures, 54(2-3), 361–370 (2001) |
| [2] | VASILIEV, V. V., BARYNIN, V. A., and RAZIN, A. F. Anisogrid composite lattice structures — development and aerospace applications. Composite Structures, 94(3), 1117–1127 (2012) |
| [3] | GIUSTO, G., TOTARO, G., SPENA, P., DE NICOLA, F., DI CAPRIO, F., ZALLO, A., GRILLI, A., MANCINI, V., KIRYENKO, S., DAS, S., and MESPOULET, S. Composite grid structure technology for space applications. Materials Today: Proceedings, 34, 332–340 (2021) |
| [4] | TOTARO, G. Multilevel Optimization of Anisogrid Structures for Aerospace Applications, Ph. D. dissertation, Delft University of Technology (2011) |
| [5] | FAN, H. L., FANG, D. N., and JIN, F. N. Mechanical properties of lattice grid composites. Acta Mechanica Sinica, 24(4), 409–418 (2008) |
| [6] | FAN, H. L. and YANG, W. An equivalent continuum method of lattice structures. Acta Mechanica Solida Sinica, 19(2), 103–113 (2006) |
| [7] | KIDANE, S., LI, G. Q., HELMS, J., PANG, S. S., and WOLDESENBET, E. Buckling load analysis of grid stiffened composite cylinders. Composites Part B: Engineering, 34(1), 1–9 (2003) |
| [8] | BURAGOHAIN, M. and VELMURUGAN, R. Buckling analysis of composite hexagonal lattice cylindrical shell using smeared stiffener model. Defence Science Journal, 59(3), 230–238 (2009) |
| [9] | ZHENG, Q., JIANG, D. Z., HUANG, C. F., SHANG, X. L., and JU, S. Analysis of failure loads and optimal design of composite lattice cylinder under axial compression. Composite Structures, 131, 885–894 (2015) |
| [10] | LI, M., LAI, C. L., ZHENG, Q., and FAN, H. L. Multi-failure analyses of carbon fiber reinforced anisogrid lattice cylinders. Aerospace Science and Technology, 100, 105777 (2020) |
| [11] | LOPATIN, A. V., MOROZOV, E. V., and SHATOV, A. V. Axial deformability of the composite lattice cylindrical shell under compressive loading: application to a load-carrying spacecraft tubular body. Composite Structures, 146, 201–206 (2016) |
| [12] | LOPATIN, A. V., MOROZOV, E. V., and SHATOV, A. V. An analytical expression for fundamental frequency of the composite lattice cylindrical shell with clamped edges. Composite Structures, 141, 232–239 (2016) |
| [13] | LOPATIN, A. V., MOROZOV, E. V., and SHATOV, A. V. Buckling of uniaxially compressed composite anisogrid lattice plate with clamped edges. Composite Structures, 157, 187–196 (2016) |
| [14] | TOTARO, G. Flexural, torsional, and axial global stiffness properties of anisogrid lattice conical shells in composite material. Composite Structures, 153, 738–445 (2016) |
| [15] | SHI, H. G., FAN, H. L., and SHAO, G. J. Equivalent continuum method for anisogrid composite lattice conical shells with equiangular, equidistant and geodesic spiral ribs. Composite Structures, 275, 114472 (2021) |
| [16] | FORMAN, S. E. and HUTCHINSON, J. W. Buckling of reticulated shell structures. International Journal of Solids and Structures, 6(7), 909–932 (1970) |
| [17] | TOTARO, G. Local buckling modelling of isogrid and anisogrid lattice cylindrical shells with triangular cells. Composite Structures, 94, 446–452 (2012) |
| [18] | TOTARO, G. Local buckling modelling of isogrid and anisogrid lattice cylindrical shells with hexagonal cells. Composite Structures, 95, 403–410 (2013) |
| [19] | MOROZOV, E. V., LOPATIN, A. V., and NESTEROV, V. A. Finite-element modelling and buckling analysis of anisogrid composite lattice cylindrical shells. Composite Structures, 93, 308–323 (2011) |
| [20] | MOROZOV, E. V., LOPATIN, A. V., and NESTEROV, V. A. Buckling analysis and design of anisogrid composite lattice conical shells. Composite Structures, 93, 3150–3162 (2011) |
| [21] | FRULLONI, E., KENNY, J. M., CONTI, P., and TORRE, L. Experimental study and finite element analysis of the elastic instability of composite lattice structures for aeronautic applications. Composite Structures, 78, 519–528 (2007) |
| [22] | BELARDI, V. G., FANELLI, P., and VIVIO, F. Structural analysis and optimization of anisogrid composite lattice cylindrical shells. Composites Part B: Engineering, 139, 203–215 (2018) |
| [23] | BELARDI, V. G., FANELLI, P., and VIVIO, F. Design, analysis and optimization of anisogrid composite lattice conical shells. Composites Part B: Engineering, 150, 184–195 (2018) |
| [24] | TONG, L. Y., TABARROK, B., and WANG, T. K. Simple solutions for buckling of orthotropic conical shells. International Journal of Solids and Structures, 29(8), 933–946 (1992) |
| [25] | TONG, L. Y. and WANG, T. K. Simple solutions for buckling of laminated conical shells. International Journal of Mechanical Sciences, 34(2), 93–111 (1992) |
| [26] | TONG, L. Y. Free vibration of composite laminated conical shells. International Journal of Mechanical Sciences, 35(1), 47–61 (1993) |
| [27] | SOFIYEV, A. H. The buckling of an orthotropic composite truncated conical shell with continuously varying thickness subject to a time dependent external pressure. Composites Part B: Engineering, 34(3), 227–233 (2003) |
| [28] | SOFIYEV, A. H. Non-linear buckling behavior of FGM truncated conical shells subjected to axial load. International Journal of Non-Linear Mechanics, 46(5), 711–719 (2011) |
| [29] | XIE, X., JIN, G. Y., YE, T. G., and LIU, Z. G. Free vibration analysis of functionally graded conical shells and annular plates using the Haar wavelet method. Applied Acoustics, 85, 130–142 (2014) |
| [30] | MEHRI, M., ASADI, H., and WANG, Q. Buckling and vibration analysis of a pressurized CNT reinforced functionally graded truncated conical shell under an axial compression using HDQ method. Computer Methods in Applied Mechanics and Engineering, 303, 75–100 (2016) |
| [31] | FAGHIH SHOJAEI, M. and ANSARI, R. Variational differential quadrature: a technique to simplify numerical analysis of structures. Applied Mathematical Modelling, 49, 705–738 (2017) |
| [32] | ANSARI, R. and TORABI, J. Numerical study on the buckling and vibration of functionally graded carbon nanotube-reinforced composite conical shells under axial loading. Composites Part B: Engineering, 95, 196–208 (2016) |
| [33] | ANSARI, R., FAGHIH SHOJAEI, M., ROUHI, H., and HOSSEINZADEH, M. A novel variational numerical method for analyzing the free vibration of composite conical shells. Applied Mathematical Modelling, 39, 2849–2860 (2015) |
| [34] | ANSARI, R., TORABI, J., and HASRATI, E. Postbuckling analysis of axially-loaded functionally graded GPL-reinforced composite conical shells. Thin-Walled Structures, 148, 106594 (2020) |
| [35] | KOITER, W. T. On the Stability of Elastic Equilibrium, Ph. D. dissertation, Delft University of Technology (1945) |
| [36] | BUDIANSKY, B. Theory of buckling and post-buckling behavior of elastic structures. Advances in Applied Mechanics 14, 1–65 (1974) |
| [37] | BYSKOV, E. Elementary Continuum Mechanics for Everyone, Springer, Netherlands (2013) |
| [38] | HENRICHSEN, S. R., WEAVER, P. M., LINDGAARD, E., and LUND, E. Post-buckling optimization of composite structures using Koiter’s method. International Journal for Numerical Methods in Engineering, 108, 902–940 (2016) |
| [39] | GOLDFELD, Y., SHEINMAN, I., and BARUCH, M. Imperfection sensitivity of conical shells. AIAA Journal, 41(3), 517–524 (2003) |
| [40] | GOLDFELD, Y. Imperfection sensitivity of laminated conical shells. International Journal of Solids and Structures, 44(3-4), 1221–1241 (2007) |
| [41] | GOLDFELD, Y. Elastic buckling and imperfection sensitivity of generally stiffened conical shells. AIAA Journal, 45(3), 721–729 (2007) |
| [42] | WHITE, S. C., RAJU, G., and WEAVER, P. M. Initial post-buckling of variable-stiffness curved panels. Journal of the Mechanics and Physics of Solids, 71, 132–155 (2014) |
| [43] | RAHMAN, T. and JANSEN, E. L. Finite element based coupled mode initial post-buckling analysis of a composite cylindrical shell. Thin-Walled Structures, 48, 25–32 (2010) |
| [44] | ANSARI, R. and TORABI, J. Semi-analytical postbuckling analysis of polymer nanocomposite cylindrical shells reinforced with functionally graded graphene platelets. Thin-Walled Structures, 144, 106248 (2019) |
| [45] | SHI, H. G., FAN, H. L., and SHAO, G. J. Dynamic theory of composite anisogrid lattice conical shells with nonconstant stiffness and density. Applied Mathematical Modelling, 115, 661–690 (2023) |
| [46] | SHARGHI, H., SHAKOURI, M., and KOUCHAKZADEH, M. A. An analytical approach for buckling analysis of generally laminated conical shells under axial compression. Acta Mechanica, 227(4), 1181–1198 (2016) |
| [47] | ABBASI, M. and GHANBARI, J. A comprehensive analytical model for global buckling analysis of general grid cylindrical structures with various cell geometries. International Journal for Computational Methods in Engineering Science and Mechanics, 22(6), 477–499 (2021) |
| [48] | ZHANG, F., PAN, F., and CHEN, Y. L. Revisiting the stiffness of lattice plates with micromechanics modeling. Composite Structures, 286, 115276 (2022) |
| [49] | VASILIEV, V. V., RAZIN, A., TOTARO, G., and DE NICOLA, F. Anisogrid conical adapters for commercial space application. Proceedings of the AIAA/CIRA 13th International Space Planes and Hypersonic Systems, American Institute of Aeronautics and Astronautics, Capua (2005) |
| [50] | SHU, C. Differential Quadrature and Its Application in Engineering, Springer, London (2000) |
| [51] | SHARGHI, H., SHAKOURI, M., and KOUCHAKZADEH, M. A. An analytical approach for buckling analysis of generally laminated conical shells under axial compression. Acta Mechanica, 227(4), 1181–1198 (2016) |
| [52] | SPAGNOLI, A. Koiter circles in the buckling of axially compressed conical shells. International Journal of Solids and Structures, 40(22), 6095–6109 (2003) |
| [53] | CIVALEK, Ö. Application of differential quadrature (DQ) and harmonic differential quadrature (HDQ) for buckling analysis of thin isotropic plates and elastic columns. Engineering Structures, 26(2), 171–186 (2004) |
| [54] | FUNG, T. C. Imposition of boundary conditions by modifying the weighting coefficient matrices in the differential quadrature method. International Journal for Numerical Methods in Engineering, 56(3), 405–432 (2003) |
| [55] | ABAQUS. ABAQUS/Standard User’s Manual, Hibbitt, Karlsson, & Sorensen, Inc. (2005) |
| [56] | MARTINEZ, O. Micromechanical Analysis and Design of an Integrated Thermal Protection System for Future Space Vehicles, Ph. D. dissertation, University of Florida (2007) |
| [57] | RIKS, E. An incremental approach to the solution of snapping and buckling problems. International Journal of Solids and Structures, 15(7), 529–551 (1979) |
| [58] | CRISFIELD, M. A. A fast incremental/iterative solution procedure that handles “snap-through”. Computers & Structures, 13, 55–62 (1981) |
| [1] | Dejuan KONG, Zhuangzhuang HE, Chengbin LIU, Chunli ZHANG. Analysis of multi-field coupling behaviors of sandwich piezoelectric semiconductor beams under thermal loadings [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(8): 1571-1590. |
| [2] | Lu LU, Min LI, Shuang WANG. Surface effects on buckling instability and large deformation of magneto-active soft beams [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(4): 617-632. |
| [3] | Chang LI, Hai QING. Size-dependent axisymmetric bending and buckling analysis of functionally graded sandwich Kirchhoff nanoplates using nonlocal strain gradient integral model [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(3): 467-484. |
| [4] | Wei WANG, Gaofei GUAN, Yongqi LI, Jiabin SUN, Zhenhuan ZHOU, Xinsheng XU. Nonlinear post-buckling modeling of a magneto-electro-elastic cylindrical shell with flexomagnetic and flexoelectric effects [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(11): 2135-2154. |
| [5] | Dali WANG, Tianli JIANG, Huliang DAI, Lin WANG. Non-planar vibration characteristics and buckling behaviors of two fluid-conveying pipes coupled with an intermediate spring [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(10): 1829-1850. |
| [6] | N. D. NGUYEN, T. N. NGUYEN. Chebyshev polynomial-based Ritz method for thermal buckling and free vibration behaviors of metal foam beams [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(5): 891-910. |
| [7] | H.M. FEIZABAD, M.H. YAS. Free vibration and buckling analysis of polymeric composite beams reinforced by functionally graded bamboo fibers [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(3): 543-562. |
| [8] | Lei WANG, Yingge LIU, Juxi HU, Weimin CHEN, Bing HAN. A non-probabilistic reliability topology optimization method based on aggregation function and matrix multiplication considering buckling response constraints [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 321-336. |
| [9] | Feixiang TANG, Shaonan SHI, Siyu HE, Fang DONG, Sheng LIU. Size-dependent vibration and buckling of porous functionally graded microplates based on modified couple stress theory in thermal environments by considering a dual power-law distribution of scale effects [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(12): 2075-2092. |
| [10] | Qiao ZHANG, Yuxin SUN. Statics, vibration, and buckling of sandwich plates with metamaterial cores characterized by negative thermal expansion and negative Poisson's ratio [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1457-1486. |
| [11] | Shan XIA, Linghui HE. Buckling morphology of glassy nematic films with staggered director field [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(11): 1841-1852. |
| [12] | Andi LAI, Bing ZHAO, Xulong PENG, Chengyun LONG. Effects of local thickness defects on the buckling of micro-beam [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(5): 729-742. |
| [13] | Chi XU, Yang LI, Mingyue LU, Zhendong DAI. Buckling analysis of functionally graded nanobeams under non-uniform temperature using stress-driven nonlocal elasticity [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(3): 355-370. |
| [14] | Shuai WANG, Jiajia MAO, Wei ZHANG, Haoming LU. Nonlocal thermal buckling and postbuckling of functionally graded graphene nanoplatelet reinforced piezoelectric micro-plate [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(3): 341-354. |
| [15] | Xinlei LI, Jianfei WANG. Effects of layer number and initial pressure on continuum-based buckling analysis of multi-walled carbon nanotubes accounting for van der Waals interaction [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(12): 1857-1872. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS