Fig. 1

Decomposition of internal forces on the rod cross section under finite deformation: (a) Engesser’s approach[41–43], (b) Timoshenko’s approach[44–45], and (c) Haringx’s approach[46–48] (color online)"

Fig. 2

Force analysis on the microelement ds (color online)"

Fig. 3

(a) The initial configuration of the arch, (b) the point contact or point-to-line contact transition stage, (c) the line contact or critical buckling stage, and (d) the post-buckling stage (color online)"

Fig. 4

Displacement-load curves of the arch under compression with (a) α0=30∘ and R=100 mm, (b) α0=45∘ and R=70.7 mm, and (c) α0=60∘ and R=57.735 mm (color online)"

Fig. 5

Deflection curves with α0=30∘ and R=100 mm in different stages (color online)"

Fig. 6

Dimensionless normal force N¯ in different stages (color online)"

Fig. 7

Dimensionless shear force Q¯ in different stages (color online)"

Fig. 8

(a) The contact pressure region (highlighted in red) and (b) the dimensionless contact pressure at (i)–(ii) the point contact stages and (iii) the line contact stage calculated by the FEM (color online)"

Fig. 9

Dimensionless moment M¯ in different stages (color online)"

Table 1

The scaling exponents of the critical load and the independent quantities"

Fig. 10

The relationships of Pcr and D with different α0 and IAR2, where the values of IAR2 are equal to 1.09×10−5, 2.13×10−5, and 3.33×10−5 (color online)"

Fig. 11

Effects of α0 and IAR2 on the dimensionless critical load P¯cr (color online)"

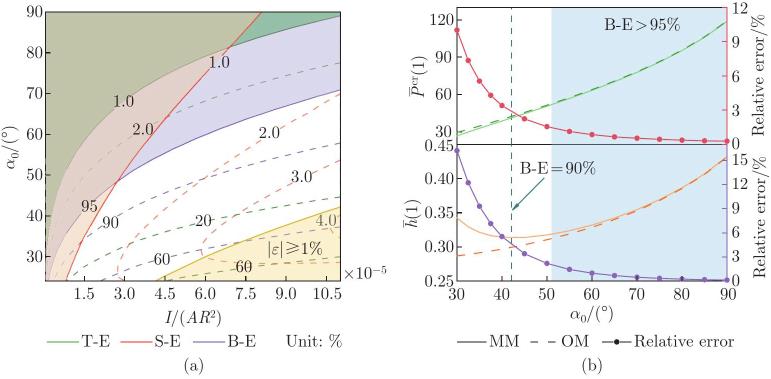
Fig. 12

(a) The relationship between the proportions of the three strain energy components at the critical buckling state and the parameters α0 and IAR2; (b) the comparison of the dimensionless critical load P¯cr and the dimensionless displacement h¯ of the rigid plate between the MM and OM when IAR2=3.33×10−5, where T-E, S-E, and B-E represent the tensile, shear, and bending strain energies, respectively (color online)"