A comprehensive investigation on nonlinear vibration andbending characteristics of bio-inspired helicoidallaminated composite structures

doi:10.1007/s10483-025-3200-7

Abstract

Abstract:

Bio-inspired helicoidal composite laminates, inspired by the intricate helical structures found in nature, present a promising frontier for enhancing the mechanical properties of structural designs. Hence, this study provides a comprehensive investigation into the nonlinear free vibration and nonlinear bending behavior of bio-inspired composite plates. The inverse hyperbolic shear deformation theory (IHSDT) of plates is employed to characterize the displacement field, with the incorporation of Green-Lagrange nonlinearity. The problem is modeled using the C⁰ finite element method (FEM), and an in-house code is developed in the MATLAB environment to solve it numerically. Various helicoidal layup configurations including helicoidal recursive (HR), helicoidal exponential (HE), helicoidal semi-circular (HS), linear helicoidal (LH), and Fibonacci helicoidal (FH) with different layup sequences and quasi-isotropic configurations are studied. The model is validated, and parametric studies are conducted. These studies investigate the effects of layup configurations, side-to-thickness ratio, modulus ratios, boundary conditions, and loading conditions at different load amplitudes on the nonlinear vibration and nonlinear bending behaviors of bio-inspired composite plates. The results show that the laminate sequence exerts a substantial impact on both nonlinear natural frequencies and nonlinear bending behaviors. Moreover, this influence varies across different side-to-thickness ratios and boundary conditions of the bio-inspired composite plate.

Key words: finite element method (FEM), nonlinear, Green-Lagrange, inverse hyperbolic shear deformation theory (IHSDT), bio-inspired composite plate, helicoidal

2010 MSC Number:

O322

S. SAURABH, R. KIRAN, D. SINGH, R. VAISH, V. S. CHAUHAN. A comprehensive investigation on nonlinear vibration andbending characteristics of bio-inspired helicoidallaminated composite structures. Applied Mathematics and Mechanics (English Edition), 2025, 46(1): 81-100.

TrendMD

Figures/Tables 14

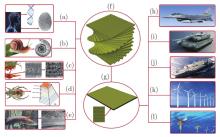
Fig. 1

Fig. 2

Fig. 3

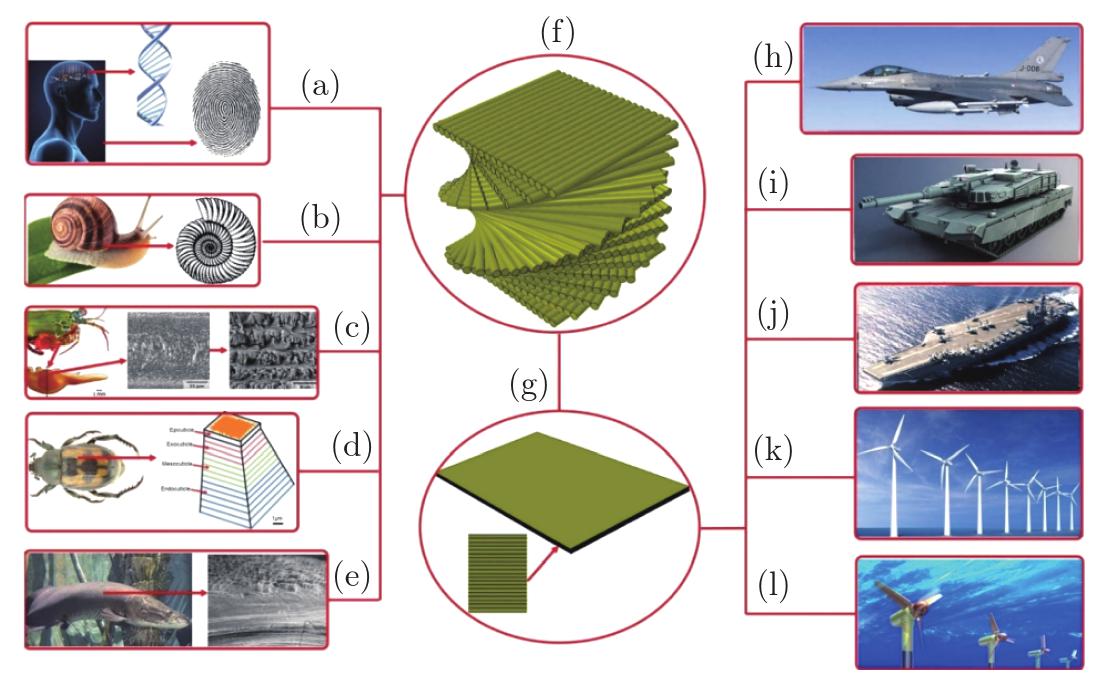
Table 1

The normalized natural frequencies ratio (ω¯nl/ω¯l) of 12-layered bio-inspired composite plate (E1/E2=10 and a/h=10) subject to the SSSS condition"

$E 1 / E 2$	$a / h$	$ω max / h$
$E 1 / E 2$	$a / h$	Layup configuration	0.2	0.4	0.6	0.8	1
10	10	HR1	1.044 7	1.181 5	1.382 4	1.428 3	1.535 5
		HR2	1.044 7	1.175 9	1.370 5	1.411 5	1.506 2
		HR3	1.044 7	1.171 7	1.360 8	1.401 7	1.493 2
		HE1	1.044 7	1.182 3	1.384 1	1.436 3	1.553 9
		HE2	1.044 7	1.178 1	1.375 5	1.430 4	1.537 2
		HE3	1.044 7	1.170 3	1.359 0	1.422 7	1.519 8
		HS1	1.044 7	1.143 5	1.302 5	1.498 9	1.450 5
		HS2	1.044 7	1.170 8	1.357 3	1.585 6	1.519 3
		HS3	1.044 7	1.167 5	1.351 3	1.577 3	1.589 1
		LH1	1.044 7	1.176 9	1.372 9	1.418 1	1.513 5
		LH2	1.044 7	1.173 7	1.366 1	1.411 0	1.501 0
		LH3	1.044 7	1.170 4	1.359 1	1.404 7	1.490 9
		FH	1.044 4	1.169 3	1.355 8	1.401 2	1.490 8
		QI	1.042 8	1.162 7	1.340 9	1.559 3	1.573 4

Table 1

Table 2

The normalized natural frequencies ratio (ω¯nl/ω¯l) of 12-layered bio-inspired composite plate (E1/E2=10 and a/h=100) subject to the SSSS condition"

$E 1 / E 2$	$a / h$	$ω max / h$
$E 1 / E 2$	$a / h$	Layup configuration	0.2	0.4	0.6	0.8	1
10	100	HR1	1.030 8	1.140 5	1.298 6	1.497 5	1.483 2
		HR2	1.030 8	1.133 7	1.284 6	1.474 5	1.456 2
		HR3	1.030 8	1.127 4	1.271 5	1.452 8	1.436 0
		HE1	1.030 8	1.141 4	1.300 5	1.500 6	1.495 4
		HE2	1.030 8	1.136 8	1.291 1	1.485 4	1.488 0
		HE3	1.030 8	1.128 3	1.273 5	1.456 6	1.476 2
		HS1	1.030 8	1.100 3	1.215 0	1.360 7	1.529 3
		HS2	1.030 8	1.123 0	1.261 0	1.433 5	1.630 6
		HS3	1.030 8	1.123 8	1.263 0	1.437 3	1.636 8
		LH1	1.030 8	1.135 4	1.288 3	1.480 8	1.469 9
		LH2	1.030 8	1.131 8	1.280 8	1.468 6	1.459 4
		LH3	1.030 8	1.128 1	1.273 0	1.455 8	1.449 4
		FH	1.032 4	1.124 8	1.265 9	1.443 8	1.435 1
		QI	1.030 8	1.118 5	1.252 0	1.419 4	1.610 9

Table 2

Table 3

The normalized natural frequencies ratio (ω¯nl/ω¯l) of 12-layered bio-inspired composite plate (E1/E2=40 and a/h=10) subject to the SSSS condition"

$E 1 / E 2$	$a / h$	$ω max / h$
$E 1 / E 2$	$a / h$	Layup configuration	0.2	0.4	0.6	0.8	1
40	10	HR1	1.074 6	1.285 7	1.262 7	1.488 1	1.489 2
		HR2	1.072 7	1.276 6	1.261 8	1.518 5	1.529 3
		HR3	1.071 9	1.271 0	1.277 8	1.578 5	1.579 5
		HE1	1.074 5	1.285 9	1.273 5	1.482 4	1.501 6
		HE2	1.072 2	1.276 6	1.272 2	1.494 8	1.501 6
		HE3	1.068 0	1.259 1	1.281 5	1.544 5	1.501 6
		HS1	1.054 7	1.205 1	1.271 6	1.327 2	1.501 6
		HS2	1.068 5	1.255 3	1.352 2	1.399 1	1.501 6
		HS3	1.064 1	1.240 8	1.394 7	1.466 4	1.501 6
		LH1	1.072 3	1.276 3	1.254 4	1.496 7	1.501 6
		LH2	1.070 8	1.270 2	1.253 3	1.512 6	1.501 6
		LH3	1.069 4	1.263 9	1.254 5	1.349 4	1.501 6
		FH	1.070 6	1.265 7	1.281 2	1.408	1.599 9
		QI	1.062 4	1.233 2	1.479 3	1.453	1.501 6

Table 3

Table 4

The normalized natural frequencies ratio (ω¯nl/ω¯l) of 12-layered bio-inspired composite plate (E1/E2=40 and a/h=100) subject to the SSSS condition"

$E 1 / E 2$	$a / h$	$ω max / h$
$E 1 / E 2$	$a / h$	Layup configuration	0.2	0.4	0.6	0.8	1
40	100	HR1	1.041 5	1.162 1	1.198 2	1.257 1	1.450 0
		HR2	1.038 8	1.151 0	1.196 7	1.252 9	1.326 8
		HR3	1.036 4	1.141 2	1.201 9	1.260 2	1.334 6
		HE1	1.042 0	1.163 9	1.205 7	1.268 7	1.449 2
		HE2	1.040 3	1.156 8	1.215 9	1.278 1	1.366 1
		HE3	1.037 1	1.144 0	1.310 0	1.295 3	1.364 2
		HS1	1.027 0	1.104 5	1.223 9	1.375 3	1.349 6
		HS2	1.035 5	1.135 9	1.286 8	1.474 0	1.686 6
		HS3	1.035 7	1.136 7	1.289 0	1.478 6	1.694 7
		LH1	1.039 6	1.154 2	1.202 9	1.258 5	1.327 9
		LH2	1.038 1	1.148 4	1.204 8	1.258 3	1.322 3
		LH3	1.036 7	1.142 6	1.207 4	1.259 2	1.320 5
		FH	1.035 5	1.137 6	1.208 8	1.268 6	1.344 1
		QI	1.033 2	1.127 1	1.269 3	1.446 6	1.648 7

Table 4

Table 5

The normalized natural frequencies ratio (ω¯nl/ω¯l) of 12-layered bio-inspired composite plate (E1/E2=10 and a/h=10) subject to the CCCC condition"

$E 1 / E 2$	$a / h$	$ω max / h$
$E 1 / E 2$	$a / h$	Layup configuration	0.2	0.4	0.6	0.8	1
10	10	HR1	1.018 2	1.071 5	1.156 7	1.269 9	1.260 5
		HR2	1.018 1	1.071 1	1.155 7	1.267 5	1.255 3
		HR3	1.018 2	1.071 5	1.156 2	1.267 6	1.257 5
		HE1	1.018 1	1.071 3	1.156 4	1.269 6	1.263 0
		HE2	1.017 9	1.070 5	1.154 5	1.266 1	1.261 2
		HE3	1.017 5	1.068 9	1.150 8	1.259 3	1.258 9
		HS1	1.015 9	1.062 3	1.136 1	1.232 9	1.248 1
		HS2	1.018 5	1.072 5	1.157 6	1.269 9	1.277 4
		HS3	1.017 2	1.067 5	1.147 3	1.252 2	1.377 7
		LH1	1.017 9	1.070 5	1.154 5	1.265 9	1.254 2
		LH2	1.017 8	1.070 0	1.153 2	1.263 5	1.251 5
		LH3	1.017 7	1.069 4	1.152 0	1.261 2	1.249 9
		FH	1.018 1	1.070 9	1.154 8	1.265 1	1.257 4
		QI	1.017	1.066 7	1.145 3	1.248 2	1.260 5

Table 5

Table 6

The normalized natural frequencies ratio (ω¯nl/ω¯l) of 12-layered bio-inspired composite plate (E1/E2=10 and a/h=100) subject to the CCCC condition"

$E 1 / E 2$	$a / h$	$ω max / h$
$E 1 / E 2$	$a / h$	Layup configuration	0.2	0.4	0.6	0.8	1
10	100	HR1	1.010 2	1.040 4	1.089 3	1.155 1	1.235 9
		HR2	1.009 1	1.039 1	1.086 5	1.150 1	1.228 2
		HR3	1.009 6	1.038 0	1.083 8	1.145 5	1.220 9
		HE1	1.010 3	1.040 7	1.090 0	1.156 4	1.237 9
		HE2	1.010 2	1.040 2	1.088 9	1.154 4	1.234 7
		HE3	1.009 9	1.039 2	1.086 6	1.150 3	1.228 3
		HS1	1.008 7	1.034 5	1.076 1	1.131 9	1.200 0
		HS2	1.010 3	1.040 6	1.089 0	1.153 4	1.231 1
		HS3	1.010 1	1.039 9	1.087 7	1.151 3	1.228 5
		LH1	1.010 0	1.039 6	1.087 5	1.152 1	1.231 2
		LH2	1.009 9	1.039 0	1.086 2	1.149 6	1.227 4
		LH3	1.009 7	1.038 3	1.084 7	1.147 0	1.223 4
		FH	1.009 5	1.037 6	1.083 1	1.144 2	1.219 0
		QI	1.010 0	1.039 3	1.086 3	1.148 9	1.224 5

Table 6

Table 7

The normalized natural frequencies ratio (ω¯nl/ω¯l) of 12-layered bio-inspired composite plate (E1/E2=40 and a/h=10) subject to the CCCC condition"

$E 1 / E 2$	$a / h$	$ω max / h$
$E 1 / E 2$	$a / h$	Layup configuration	0.2	0.4	0.6	0.8	1
40	10	HR1	1.038 9	1.153 5	1.171 2	1.227 4	1.353 4
		HR2	1.039 5	1.154 9	1.176	1.237 1	1.398 7
		HR3	1.040 5	1.157 2	1.190 8	1.260 5	1.457 9
		HE1	1.038 3	1.151 3	1.171 8	1.201 1	1.345 4
		HE2	1.037 6	1.148 2	1.172 7	1.351 1	1.356 9
		HE3	1.036 0	1.141 5	1.177 7	1.245 1	1.390 7
		HS1	1.030 9	1.119 8	1.181 7	1.218 5	1.263 4
		HS2	1.037 4	1.144 8	1.209 3	1.238 0	1.267 2
		HS3	1.031 9	1.124 3	1.268 6	1.269 9	1.300 4
		LH1	1.038 5	1.151 5	1.167 7	1.214 3	1.376 9
		LH2	1.038 4	1.150 6	1.168 6	1.215 9	1.389 3
		LH3	1.038 2	1.149 6	1.712 0	1.219 8	1.412 4
		FH	1.039 8	1.154 3	1.191 4	1.258 7	1.474 8
		QI	1.032 1	1.124 2	1.266 4	1.261 6	1.294 5

Table 7

Table 8

The normalized natural frequencies ratio (ω¯nl/ω¯l) of 12-layered bio-inspired composite plate (E1/E2=40 and a/h=100) subject to the CCCC condition"

$E 1 / E 2$	$a / h$	$ω max / h$
$E 1 / E 2$	$a / h$	Layup configuration	0.2	0.4	0.6	0.8	1
40	100	HR1	1.010 7	1.042 7	1.096 4	1.092 6	1.117 5
		HR2	1.010 2	1.040 8	1.091 7	1.091 4	1.114 3
		HR3	1.009 8	1.039 0	1.087 2	1.094 4	1.117 9
		HE1	1.010 8	1.043 2	1.097 6	1.095 8	1.122 9
		HE2	1.010 6	1.042 4	1.095 5	1.099 9	1.125 8
		HE3	1.010 2	1.040 8	1.091 3	1.111 0	1.135 7
		HS1	1.008 5	1.003 6	1.074 3	1.129 3	1.196 7
		HS2	1.010 8	1.042 5	1.093 2	1.160 2	1.241 1
		HS3	1.010 4	1.041 2	1.090 6	1.156 3	1.236 0
		LH1	1.010 4	1.041 6	1.093 5	1.093 9	1.117 0
		LH2	1.010 2	1.040 6	1.091 2	1.094 6	1.116 7
		LH3	1.009 9	1.039 6	1.088 8	1.096 0	1.117 3
		FH	1.009 7	1.038 5	1.086 0	1.097 9	1.122 2
		QI	1.010 3	1.040 5	1.088 9	1.153 2	1.230 8

Table 8

Fig. 4

Fig. 5

Fig. 6

References 55

[1]	DOINEAU, E., CATHALA, B., BENEZET, J. C., BRAS, J., and LE MOIGNE, N. Development of bio-inspired hierarchical fibres to tailor the fibre/matrix interphase in (bio)composites. Polymers, 13(5), 804 (2021)
[2]	STUDART, A. R. Towards high-performance bioinspired composites. Advanced Materials, 24(37), 5024–5044 (2012)
[3]	HA, N. S. and LU, G. A review of recent research on bio-inspired structures and materials for energy absorption applications. Composites Part B: Engineering, 181, 107496 (2020)
[4]	WEGST, U. G. K., BAI, H., SAIZ, E., TOMSIA, A. P., and RITCHIE, R. O. Bioinspired structural materials. Nature Materials, 14(1), 23–36 (2014)
[5]	BAR-ON, B., BAYERLEIN, B., BLUMTRITT, H., and ZLOTNIKOV, I. Dynamic response of a single interface in a biocomposite structure. Physical Review Letters, 115(23), 238001 (2015)
[6]	CHEN, J., ZU, Q., WU, G., XIE, J., and TUO, W. Review of beetle forewing structures and their biomimetic applications in China: (II) on the three-dimensional structure, modeling and imitation. Materials Science and Engineering C: Materials for Biological Applications, 55, 620–633 (2015)
[7]	MOHAMED, S. A., MOHAMED, N., and ELTAHER, M. A. Bending, buckling and linear vibration of bio-inspired composite plates. Ocean Engineering, 259, 111851 (2022)
[8]	HEINEMANN, F., LAUNSPACH, M., GRIES, K., and FRITZ, M. Gastropod nacre: structure, properties and growth biological, chemical and physical basics. Biophysical Chemistry, 153(2-3), 126–153 (2011)
[9]	SUKSANGPANYA, N., YARAGHI, N. A., KISAILUS, D., and ZAVATTIERI, P. Twisting cracks in Bouligand structures. Journal of the Mechanical Behavior of Biomedical Materials, 76, 38–57 (2017)
[10]	MENCATTELLI, L. and PINHO, S. T. Realising bio-inspired impact damage-tolerant thin-ply CFRP Bouligand structures via promoting diffused sub-critical helicoidal damage. Composites Science and Technology, 182 (2019)
[11]	MILLIRON, G. W., KISAILUS, D., WU, J., and GARAY, J. University of California Riverside Lightweight Impact-Resistant Composite Materials: Lessons from Mantis Shrimp, Ph.D. dissertation, University of Californic (2012)
[12]	TADAYON, M., AMINI, S., MASIC, A., and MISEREZ, A. The mantis shrimp saddle: a biological spring combining stiffness and flexibility. Advanced Functional Materials, 25(41), 6437–6447 (2015)
[13]	RAMAKRISHNA, D. and MURALI, G. B. Bio-inspired 3D-printed lattice structures for energy absorption applications: a review. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials-Design and Applications, 237(3), 503–542 (2022)
[14]	GARULLI, T., KATAFIASZ, T. J., GREENHALGH, E. S., and PINHO, S. T. A novel bio-inspired microstructure for improved compressive performance of multidirectional CFRP laminates. Composites Part B: Engineering, 264, 110867 (2023)
[15]	CHOUHAN, G. and MURALI, G. B. Uniform and graded bio-inspired gyroid lattice: effects of post-curing and print orientation on mechanical property. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials-Design and Applications, 238(5), 810–828 (2024)
[16]	GRUNENFELDER, L. K., SUKSANGPANYA, N., SALINAS, C., MILLIRON, G., YARAGHI, N., HERRERA, S., EVANS-LUTTEROOT, K., NUTT, S. R., ZAVATTIERI, P., and KISAILUS, D. Bio-inspired impact-resistant composites. Acta Biomater, 10(9), 3997–4008 (2014)
[17]	CHENG, L., THOMAS, A., GLANCEY, J. L., and KARLSSON, A. M. Mechanical behavior of bio-inspired laminated composites. Composites Part A: Applied Science and Manufacturing, 42(2), 211–220 (2011)
[18]	JIANG, H., REN, Y., LIU, Z., ZHANG, S., and LIN, Z. Low-velocity impact resistance behaviors of bio-inspired helicoidal composite laminates with non-linear rotation angle-based layups. Composite Structures, 214, 463–475 (2019)
[19]	APICHATTRABRUT, T. and RAVI-CHANDAR, K. Helicoidal composites. Mechanics of Advanced Materials and Structures, 13(1), 61–76 (2006)
[20]	HAZZARD, M. K., HALLETT, S., CURTIS, P. T., IANNUCCI, L., and TRASK, R. S. Effect of fibre orientation on the low velocity impact response of thin Dyneema composite laminates. International Journal of Impact Engineering, 100, 35–45 (2017)
[21]	GINZBURG, D., PINTO, F., IERVOLINO, O., and MEO, M. Damage tolerance of bio-inspired helicoidal composites under low velocity impact. Composite Structures, 161, 187–203 (2017)
[22]	SHANG, J. S., NGERN, N. H. H., and TAN, V. B. C. Crustacean-inspired helicoidal laminates. Composites Science and Technology, 128, 222–232 (2016)
[23]	KARTHIKEYAN, K., KAZEMAHVAZI, S., and RUSSELL, B. P. Optimal fibre architecture of soft-matrix ballistic laminates. International Journal of Impact Engineering, 88, 227–237 (2016)
[24]	ASKARINEJAD, S. and RAHBAR, N. Mechanics of bioinspired lamellar structured ceramic/polymer composites: experiments and models. International Journal of Plasticity, 107, 122–149 (2018)
[25]	LIU, J. L., LEE, H. P., and TAN, V. B. C. Effects of inter-ply angles on the failure mechanisms in bioinspired helicoidal laminates. Composites Science and Technology, 165, 282–289 (2018)
[26]	ABIR, M. R., TAY, T. E., and LEE, H. P. On the improved ballistic performance of bio-inspired composites. Composites Part A: Applied Science and Manufacturing, 123, 59–70 (2019)
[27]	BAHMANI, A., LI, G., WILLETT, T. L., and MONTESANO, J. Three-dimensional micromechanical assessment of bio-inspired composites with non-uniformly dispersed inclusions. Composite Structures, 212, 484–499 (2019)
[28]	YANG, F., XIE, W., and MENG, S. Global sensitivity analysis of low-velocity impact response of bio-inspired helicoidal laminates. International Journal of Mechanical Sciences, 187, 106110 (2020)
[29]	WANG, D., ZAHERI, A., RUSSELL, B., ESPINOSA, H., and ZAVATTIERI, P. Fiber reorientation in hybrid helicoidal composites. Journal of the Mechanical Behavior of Biomedical Materials, 110, 103914 (2020)
[30]	LIU, J. L., SINGH, A. K., LEE, H. P., TAY, T. E., and TAN, V. B. C. The response of bio-inspired helicoidal laminates to small projectile impact. International Journal of Impact Engineering, 142, 103608 (2020)
[31]	CHEW, E., LIU, J. L., TAY, T. E., TRAN, L. Q. N., and TAN, V. B. C. Improving the mechanical properties of natural fibre reinforced laminates composites through biomimicry. Composite Structures, 258, 113208 (2021)
[32]	WANG, M., XU, Y. G., QIAO, P., and LI, Z. M. Buckling and free vibration analysis of shear deformable graphene-reinforced composite laminated plates. Composite Structures, 280, 114854 (2022)
[33]	LIU, J. L., MENCATTELLI, L., ZHI, J., CHUA, P. Y., TAY, T. E., and TAN, V. B. C. Lightweight, fiber-damage-resistant, and healable bio-inspired glass-fiber reinforced polymer laminate. Polymers, 14(3), 475 (2022)
[34]	SHARMA, A., BELARBI, M. O., GARG, A., and LI, L. Bending analysis of bio-inspired helicoidal/Bouligand laminated composite plates. Mechanics of Advanced Materials and Structures, 31, 5326–5340 (2023)
[35]	CHEN, J., ZHANG, X., OKABE, Y., SAITO, K., GUO, Z., and PAN, L. The deformation mode and strengthening mechanism of compression in the beetle elytron plate. Materials and Design, 131, 481–486 (2017)
[36]	ZHANG, X. M., XIE, J., CHEN, J. X., OKABE, Y., PAN, L. C., and XU, M. Y. The beetle elytron plate: a lightweight, high-strength and buffering functional-structural bionic material. Scientific Reports, 7, 4440 (2017)
[37]	WU, Y., LIU, Q., FU, J., LI, Q., and HUI, D. Dynamic crash responses of bio-inspired aluminum honeycomb sandwich structures with CFRP panels. Composites Part B: Engineering, 121, 122–133 (2017)
[38]	SUN, Z., LI, D., ZHANG, W., SHI, S., and GUO, X. Topological optimization of biomimetic sandwich structures with hybrid core and CFRP face sheets. Composites Science and Technology, 142, 79–90 (2017)
[39]	THAKUR, B. R., VERMA, S., SINGH, B. N., and MAITI, D. K. Dynamic analysis of folded laminated composite plate using nonpolynomial shear deformation theory. Aerospace Science and Technology, 106, 106083 (2020)
[40]	GUPTA, A. and GHOSH, A. Isogeometric static and dynamic analysis of laminated and sandwich composite plates using nonpolynomial shear deformation theory. Composites Part B: Engineering, 176, 107295 (2019)
[41]	SAYYAD, A. S. and GHUGAL, Y. M. On the free vibration analysis of laminated composite and sandwich plates: a review of recent literature with some numerical results. Composite Structures, 129, 177–201 (2015)
[42]	ABRATE, S. and DI SCIUVA M. Equivalent single layer theories for composite and sandwich structures: a review. Composite Structures, 179, 482–494 (2017)
[43]	VERMA, S., THAKUR, B. R., SINGH, B. N., and MAITI, D. K. Geometrically nonlinear flexural analysis of multilayered composite plate using polynomial and non-polynomial shear deformation theories. Aerospace Science and Technology, 112, 106635 (2021)
[44]	GROVER, N., MAITI, D. K., and SINGH, B. N. A new inverse hyperbolic shear deformation theory for static and buckling analysis of laminated composite and sandwich plates. Composite Structures, 95, 667–675 (2013)
[45]	SINGH, D., KIRAN, R., and VAISH, R. Vibration and buckling analysis of agglomerated CNT composite plates via isogeometric analysis using non-polynomial shear deformation theory. European Journal of Mechanics-A/Solids, 98, 104892 (2023)
[46]	SHUFRIN, I., RABINOVITCH, O., and EISENBERGER, M. A semi-analytical approach for the geometrically nonlinear analysis of trapezoidal plates. International Journal of Mechanical Sciences, 52(12), 1588–1596 (2010)
[47]	DASH, P. and SINGH, B. N. Static response of geometrically nonlinear laminated composite plates having uncertain material properties. Mechanics of Advanced Materials and Structures, 22(4), 269–280 (2015)
[48]	TRAN, L. V., LEE, J., NGUYEN-VAN, H., NGUYEN-XUAN, H., and WAHAB, M. A. Geometrically nonlinear isogeometric analysis of laminated composite plates based on higher-order shear deformation theory. International Journal of Non-linear Mechanics, 72, 42–52 (2015)
[49]	PHUNG-VAN, P., NGUYEN-THOI, T., BUI-XUAN, T., and LIEU-XUAN, Q. A cell-based smoothed three-node Mindlin plate element (CS-FEM-MIN3) based on the C⁰-type higher-order shear deformation for geometrically nonlinear analysis of laminated composite plates. Computational Materials Science, 96(PB), 549–558 (2015)
[50]	ANSARI, R., HASSANI, R., GHOLAMI, R., and ROUHI, H. Nonlinear bending analysis of arbitrary-shaped porous nanocomposite plates using a novel numerical approach. International Journal of Non-linear Mechanics, 126, 103556 (2020)
[51]	BENNACEUR, M. A. and XU, Y. Application of the natural element method for the analysis of composite laminated plates. Aerospace Science and Technology, 87, 244–253 (2019)
[52]	SINGH, G., and RAO, Y. V. K. S. Large deflection behaviour of thick composite plates. Composite Structures, 8(1), 13–29 (1987)
[53]	REDDY, J. N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, CRC Press, Florida (2004)
[54]	LE-MANH, T., LUU-ANH, T., and LEE, J. Isogeometric analysis for flexural behavior of composite plates considering large deformation with small rotations. Mechanics of Advanced Materials and Structures, 23(3), 328–336 (2016)
[55]	DASH, P. and SINGH, B. N. Geometrically nonlinear bending analysis of laminated composite plate. Communications in Nonlinear Science and Numerical Simulation, 15(10), 3170–3181 (2010)