Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (6): 1029-1048.doi: https://doi.org/10.1007/s10483-025-3263-6
Previous Articles Next Articles
Jie JING1, Xiaoye MAO1,2,†( ), Hu DING1,2, Honggang LI3, Liqun CHEN1,2
), Hu DING1,2, Honggang LI3, Liqun CHEN1,2
Received:2025-01-26
Revised:2025-03-26
Published:2025-06-05
Contact:
Xiaoye MAO E-mail: xmao3@shu.edu.cnSupported by:2010 MSC Number:
Jie JING, Xiaoye MAO, Hu DING, Honggang LI, Liqun CHEN. Modeling and mechanism of vibration reduction of pipes by visco-hyperelastic materials. Applied Mathematics and Mechanics (English Edition), 2025, 46(6): 1029-1048.
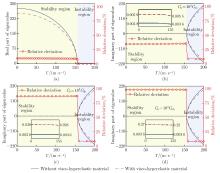
Fig. 5
Influence of C6 on the real and imaginary parts of the first-order and their relative deviations of the plain steel pipe and laminated pipe: (a) the real parts of the first-order and their relative deviations; the imaginary parts and their relative deviations when (b) C6=102C6b, (c) C6=103C6b, and (d) C6=104C6b (color online)"
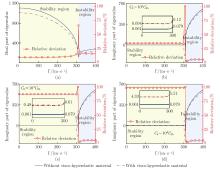
Fig. 6
Influence of C6 on the real and imaginary parts of the second-order and their relative deviations of the plain steel pipe and laminated pipe: (a) the real parts of the second-order and their relative deviations; the imaginary parts and their relative deviations when (b) C6=102C6b, (c) C6=103C6b, and (d) C6=104C6b (color online)"
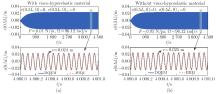
Fig. 9
Forced vibration responses of the midpoint resonances of the laminated pipe and plain steel pipe: (a) analytical results and numerical verification of the responses of the laminated pipe; (b) analytical results and numerical verification of the responses of the plain steel pipe (color online)"
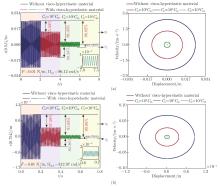
Fig. 11
Time history responses and phase trajectories of the first two orders resonances of pipes under different C6 conditions: (a) the first-order resonance response and phase trajectory at 0.5L of the pipes; (b) the second-order resonance responses and phase trajectory at 0.75L of the pipes (color online)"
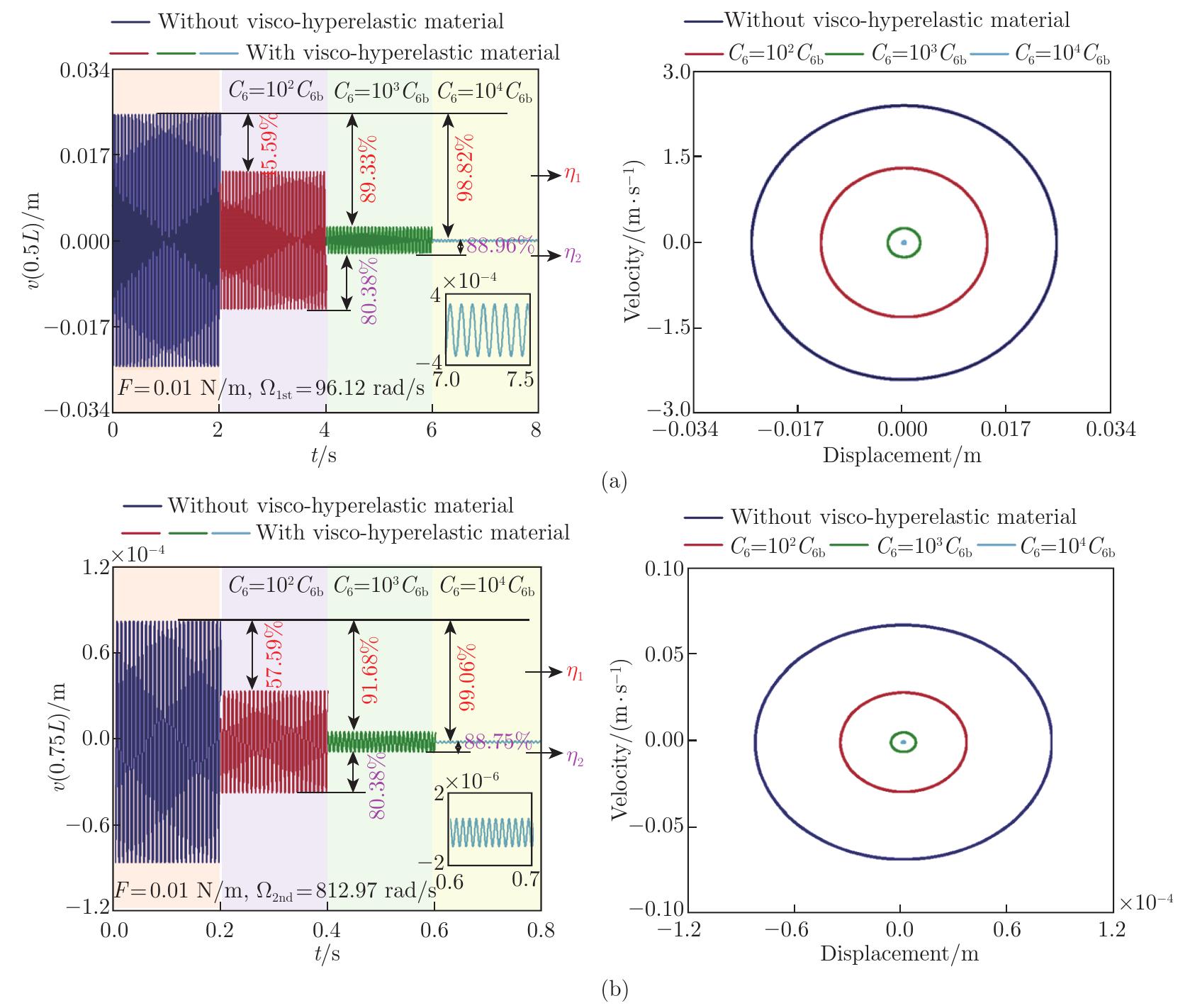
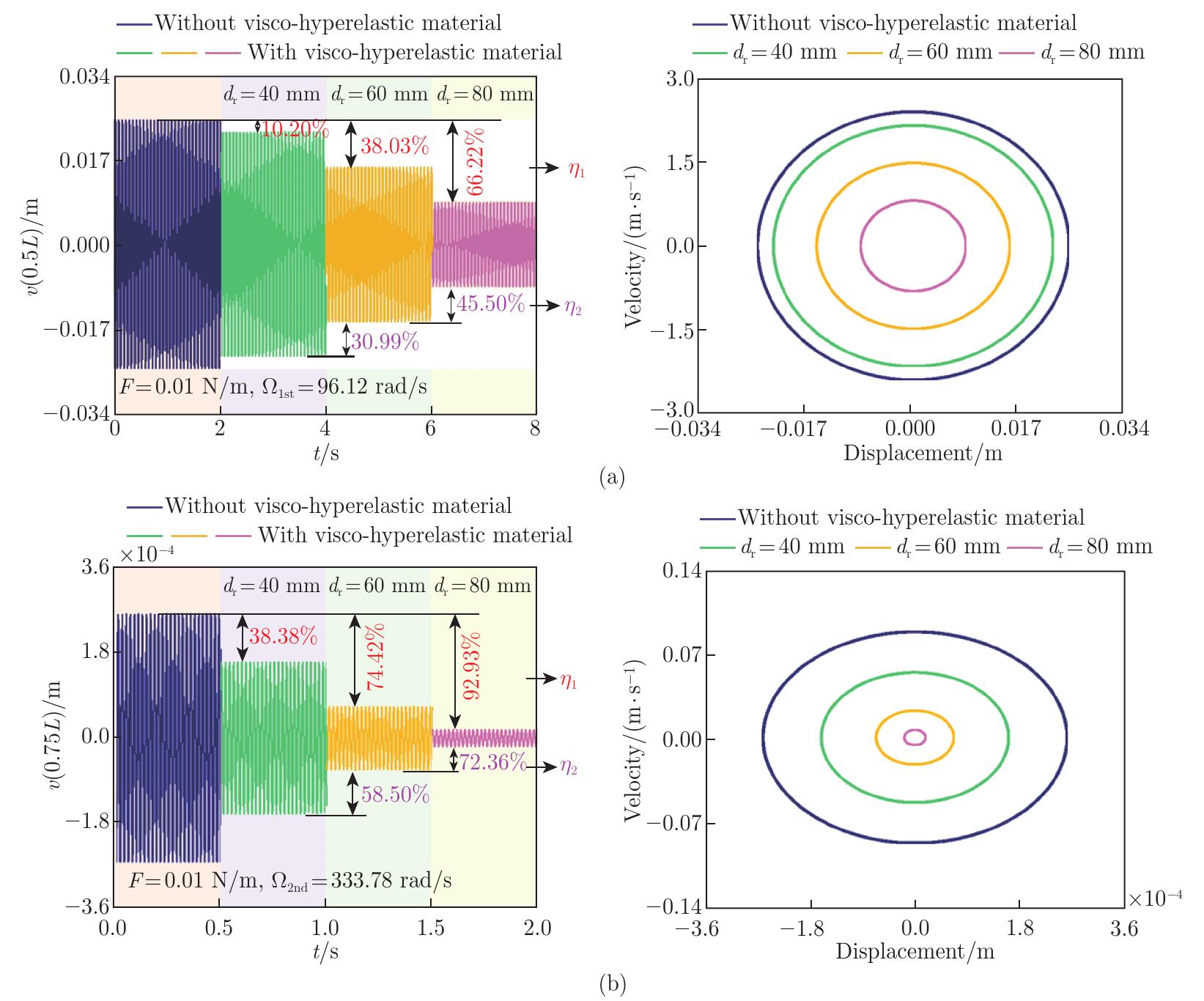
Fig. 13
Time history responses and phase trajectories of the first two orders resonances of pipes under different dr: (a) the first-order resonance response and phase trajectory at 0.5L of pipes; (b) the second-order resonance responses and phase trajectory at the 0.75L of pipes (color online)"
| [1] | GUO, X. M., CAO, Y. M., MA, H., XIAO, C. L., and WEN, B. C. Dynamic analysis of an L-shaped liquid-filled pipe with interval uncertainty. International Journal of Mechanical Sciences, 217, 107040 (2022) |
| [2] | GAO, P. X., YU, T., ZHANG, Y. L., WANG, J., and ZHAI, J. Y. Vibration analysis and control technologies of hydraulic pipeline system in aircraft: a review. Chinese Journal of Aeronautics, 34(4), 83–114 (2021) |
| [3] | JI, W. H., SUN, W., DU, D. X., and CAO, Y. H. Dynamics modeling and stress response solution for liquid-filled pipe system considering both fluid velocity and pressure fluctuations. Thin-Walled Structures, 188, 110831 (2023) |
| [4] | TANG, Y., ZHANG, H. J., CHEN, L. Q., DING, Q., GAO, Q., and YANG, T. Recent progress on dynamics and control of pipes conveying fluid. Nonlinear Dynamics, 113, 6253–6315 (2025) |
| [5] | DING, H. and JI, J. C. Vibration control of fluid-conveying pipes: a state-of-the-art review. Applied Mathematics and Mechanics (English Edition), 44(9), 1423–1456 (2023) https://doi.org/10.1007/s10483-023-3023-9 |
| [6] | HIRUTA, T., ISHIHARA, H., HOSOYA, N., MAEDA, S., TAKAGI, K., and KAJIWARA, I. Active vibration control for thin curved structures using dielectric elastomer actuators. Smart Materials and Structures, 33(3), 035047 (2024) |
| [7] | ZHANG, Y., SUN, W., ZHANG, H., DU, D. X., and XU, K. P. Active vibration control of fluid-conveying pipelines: theoretical and experimental studies. International Journal of Mechanical Sciences, 270, 109106 (2024) |
| [8] | XUE, C., XIA, Z. W., LAO, X. S., and YANG, Z. Q. Nonlinear analysis of the semi-active particle damping vibration isolation system based on fractional-order theory. Engineering Computations, 40(3), 594–614 (2023) |
| [9] | JI, H., HUANG, Y. Q., NIE, S. L., YIN, F. L., and DAI, Z. Y. Research on semi-active vibration control of pipeline based on magneto-rheological damper. Applied Sciences, 10(7), 2541 (2020) |
| [10] | GARRIDO, H., CURADELLI, O., and AMBROSINI, D. Control of relative vibration between flexible appendages using passive and semi-active isolation. Engineering Structures, 152, 819–831 (2017) |
| [11] | MACIEL, V. S. F., KHEIRI, M., and FRANZINI, G. R. Passive suppression of flow-induced vibrations of a cantilevered pipe discharging fluid using non-linear vibration absorbers. International Journal of Non-Linear Mechanics, 144, 104053 (2022) |
| [12] | MIRHASHEMI, S., SAEIDIHA, M., and AHMADI, H. Dynamics of a harmonically excited nonlinear pipe conveying fluid equipped with a local nonlinear energy sink. Communications in Nonlinear Science and Numerical Simulation, 118, 107035 (2023) |
| [13] | PHILIP, R., SANTHOSH, B., BALARAM, B., and AWREJCEWICZ, J. Vibration control in fluid conveying pipes using NES with nonlinear damping. Mechanical Systems and Signal Processing, 194, 110250 (2023) |
| [14] | ZHANG, B. L., HAN, Q. L., and ZHANG, X. M. Recent advances in vibration control of offshore platforms. Nonlinear Dynamics, 89(2), 755–771 (2017) |
| [15] | WANG, L. K., NAGARAJAIAH, S., ZHOU, Y., and SHI, W. X. Experimental study on adaptive-passive tuned mass damper with variable stiffness for vertical human-induced vibration control. Engineering Structures, 280, 115714 (2023) |
| [16] | GENG, X. F., DING, H., JI, J. C., WEI, K. X., JING, X. J., and CHEN, L. Q. A state-of-the-art review on the dynamic design of nonlinear energy sinks. Engineering Structures, 313, 118228 (2024) |
| [17] | GAO, P. X., ZHANG, Y. L., LIU, X. F., YU, T., and WANG, J. Vibration analysis of aero parallel-pipeline systems based on a novel reduced order modeling method. Journal of Mechanical Science and Technology, 34(8), 3137–3146 (2020) |
| [18] | GUO, X. M., MA, H., GE, H., CHEN, S., and WEN, B. C. Vibration transmission characteristics analysis of a flexible casing-multiple pipes system. Mechanical Systems and Signal Processing, 217, 111536 (2024) |
| [19] | WANG, Z. C., GAO, P. X., ZHOU, Z. D., TIJSSELING, A. S., QU, Y. Z., YAN, W. J., YUEN, K. V., and CHENG, S. S. A numerically stable flexural dynamics model of complex multi-span fluid-conveying pipes with flexible components and its application to clamp stiffness identification. Thin-Walled Structures, 195, 111488 (2024) |
| [20] | CHEN, W. J., CAO, Y. M., GUO, X. M., MA, H., WEN, B. C., and WANG, B. Semi-analytical dynamic modeling and fluid-structure interaction analysis of L-shaped pipeline. Thin-Walled Structures, 196, 111485 (2024) |
| [21] | LI, X. H., HU, Y. P., and HAN, Z. Y. Fatigue condition assessment of subsea pipelines under vortex induced vibration and cyclical lateral displacement. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 45(4), 9941–9957 (2023) |
| [22] | MA, H. W., SUN, W., JI, W. H., ZHANG, Y., LIU, X. F., and LIU, H. H. Dynamic modeling and vibration analysis of planar pipeline with partial constrained layer damping treatment: theoretical and experimental studies. Composite Structures, 323, 117476 (2023) |
| [23] | MA, H. W., SUN, W., WANG, D., DU, D. X., LIU, X. F., and LIN, J. Z. Finite element modeling of straight pipeline with partially attached viscoelastic damping patch based on variable thickness laminated element. Composite Structures, 314, 116944 (2023) |
| [24] | PRAHARAJ, R. K. and DATTA, N. Dynamic response of fractionally damped two-layered viscoelastic plate. Mechanics Based Design of Structures and Machines, 52(1), 36–53 (2022) |
| [25] | WANG, Y., FANG, Y. M., LI, L., ZHANG, D. G., LIAO, W. H., and FANG, J. S. Dynamic modeling and vibration suppression of a rotating flexible beam with segmented active constrained layer damping treatment. Aerospace, 10(12), 1010 (2023) |
| [26] | GRÖHLICH, M., BÖSWALD, M., and WALLASCHEK, J. Viscoelastic damping design — a novel approach for shape optimization of constrained layer damping treatments at different ambient temperatures. Journal of Sound and Vibration, 555, 117703 (2023) |
| [27] | GUPTA, A., PANDA, S., and REDDY, R. S. Damping capabilities of viscoelastic composites for active/passive constrained layer damping of the plate vibration: a comparative study. Journal of Vibration Engineering & Technologies, 12(1), 891–908 (2023) |
| [28] | ZHANG, R. F., SUN, W., LUO, H. T., MA, H. W., and ZHANG, H. Finite element dynamic modeling and vibration reduction analysis of the double-lap bolted thin plate with partially attached constrained layer damping. Thin-Walled Structures, 196, 111522 (2024) |
| [29] | CHEN, L. H. and HUANG, S. C. Vibrations of a cylindrical shell with partially constrained layer damping (CLD) treatment. International Journal of Mechanical Sciences, 41(12), 1485–1498 (1999) |
| [30] | KHALFI, B., NASRAOUI, M. T., CHAKHARI, J., ROSS, A., and CHAFRA, M. Dynamic behavior of cylindrical shell with partial constrained viscoelastic layer damping under an impact load. Acta Mechanica, 234(5), 2125–2143 (2023) |
| [31] | CUI, Z. N., YU, X. G., RAN, Z. Q., LIU, J. M., LI, C. Q., and GAO, L. Vibration reduction characteristics and vibration control of aviation hydraulic pipeline by hard coating. Coatings, 12(6), 775 (2022) |
| [32] | CUI, Z. N., LIU, J. Q., YU, X. G., RAN, Z. Q., ZHANG, J. B., and ZHANG, X. L. Research on the vibration characteristics of aviation hydraulic clamp and pipeline based on hard coating. Coatings, 12(2), 132 (2022) |
| [33] | ZI, B., JIANG, F., WU, Y. W., BAI, H. B., TANG, Y., and LU, C. H. Analysis and experimental research on vibration reduction in ship high-temperature pipeline based on long coated damping structure. Journal of Marine Science and Engineering, 9(8), 838 (2021) |
| [34] | ZHANG, Y. L., GAO, P. X., LIU, X. F., YU, T., and HUANG, Z. H. Fluid-induced vibration of a hydraulic pipeline with piezoelectric active constrained layer-damping materials. Coatings, 11(7), 757 (2021) |
| [35] | MA, H. W., SUN, W., JI, W. H., LIU, X. F., LIU, H. H., and DU, D. X. Nonlinear vibration analysis of Z-shaped pipes with CLD considering amplitude-dependent characteristics of clamps. International Journal of Mechanical Sciences, 262, 108739 (2024) |
| [36] | MA, H. W., JI, W. H., LIU, H. H., and SUN, W. Natural frequencies and stability for Z-shaped fluid-conveying pipes with constrained-layer damping—semi-analytic modeling with experimental validation. Mechanical Systems and Signal Processing, 214, 111404 (2024) |
| [37] | YANG, L. M., SHIM, V. P. W., and LIM, C. T. A visco-hyperelastic approach to modelling the constitutive behaviour of rubber. International Journal of Impact Engineering, 24(6), 545–560 (2000) |
| [38] | WANG, Y. B. and ZHU, W. D. Nonlinear transverse vibration of a hyperelastic beam under harmonic axial loading in the subcritical buckling regime. Applied Mathematical Modelling, 94, 597–618 (2021) |
| [39] | WANG, Y. B. and ZHU, W. D. Supercritical nonlinear transverse vibration of a hyperelastic beam under harmonic axial loading. Communications in Nonlinear Science and Numerical Simulation, 112, 106536 (2022) |
| [40] | KHANIKI, H. B., GHAYESH, M. H., CHIN, R., and AMABILI, M. Hyperelastic structures: a review on the mechanics and biomechanics. International Journal of Non-Linear Mechanics, 148, 104275 (2023) |
| [41] | ALI, A., HOSSEINI, M., and SAHARI, B. B. A review and comparison on some rubber elasticity models. Journal of Scientific & Industrial Research, 69(7), 495–500 (2010) |
| [42] | BABAEI, H. and ŻUR, K. K. On the pressure-deflection relations and instability of carbon-based composite nonlinear pipes. Engineering Analysis with Boundary Elements, 151, 624–638 (2023) |
| [43] | MIRJAVADI, S. S., FORSAT, M., and BADNAVA, S. Nonlinear modeling and dynamic analysis of bioengineering hyper-elastic tubes based on different material models. Biomechanics and Modeling in Mechanobiology, 19(3), 971–983 (2019) |
| [44] | ZHOU, X. Q., YU, D. Y., SHAO, X. Y., ZHANG, S. Q., and WANG, S. Research and applications of viscoelastic vibration damping materials: a review. Composite Structures, 136, 460–480 (2016) |
| [45] | ABDUL HAMID, M. I., ABD FATAH, A. Y., MAZLAN, S. A., UBAIDILLAH, U., IMADUDDIN, F., and NORDIN, N. A. Force and stiffness behavior of natural rubber based magnetorheological elastomer bushing. International Journal of Applied Electromagnetics and Mechanics, 71, 1–19 (2023) |
| [46] | ANAND, V. A catalog of pressure and deformation profile for thin walled hyperelastic tubes conveying inertialess flow and undergoing large deformation. Thin-Walled Structures, 193, 111216 (2023) |
| [47] | GUO, Y., LI, J. A., ZHU, B., and LI, Y. H. Nonlinear dynamical model of hyperelastic pipes conveying fluid with finite deformation: roles of hyperelasticity and nonlinearity. Nonlinear Dynamics, 111(15), 13691–13708 (2023) |
| [48] | GUO, Y., ZHU, B., LI, J. A., and LI, Y. H. Nonlinear dynamics of cantilevered hyperelastic pipes conveying fluid: comparative study of linearelasticity and hyperelasticity. Communications in Nonlinear Science and Numerical Simulation, 135, 108081 (2024) |
| [49] | LI, M., XU, Q., CHEN, X. C., ZHANG, X. L., and LI, Y. H. Modeling and modal analysis of non-uniform multi-span oil-conveying pipes with elastic foundations and attachments. Applied Mathematical Modelling, 88, 661–675 (2020) |
| [50] | MAO, X. Y., JING, J., DING, H., and CHEN, L. Q. Dynamics of axially functionally graded pipes conveying fluid. Nonlinear Dynamics, 111(12), 11023–11044 (2023) |
| [51] | RAVICHANDRAN, A. and MOHANTY, P. K. Experimental and computational techniques of free in-plane vibration of a fixed support curved beam with a single crack. Journal of Vibration Engineering & Technologies, 12(2), 2517–2540 (2023) |
| [52] | DING, H., YAN, Q. Y., and ZU, J. W. Chaotic dynamics of an axially accelerating viscoelastic beam in the supercritical regime. International Journal of Bifurcation and Chaos, 24(5), 1450062 (2014) |
| [53] | SUN, G., LI, H., WANG, T., and XU, Q. Out-of-plane free vibration analysis of continuous curved girders with combined linetypes using differential quadrature element method. International Journal of Structural Stability and Dynamics, 22(5), 2250060 (2022) |
| [54] | WANG, X. W. and WANG, Y. L. Free vibration analysis of multiple-stepped beams by the differential quadrature element method. Applied Mathematics and Computation, 219(11), 5802–5810 (2013) |
| [55] | MAO, X. Y., DING, H., and CHEN, L. Q. Vibration of flexible structures under nonlinear boundary conditions. Journal of Applied Mechanics, 84, 111006 (2017) |
| [56] | MAO, X. Y., DING, H., and CHEN, L. Q. Bending vibration control of pipes conveying fluids by nonlinear torsional absorbers at the boundary. Science China Technological Sciences, 64(8), 1690–1704 (2021) |
| [1] | M. GHOLAMI, M. EFTEKHARI. Nonlinear forced vibration in a subcritical regime of a porous functionally graded pipe conveying fluid with a retaining clip [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(1): 101-122. |
| [2] | Xingzhong WANG, Shiteng RUI, Shaokun YANG, Weiquan ZHANG, Fuyin MA. A low-frequency pure metal metamaterial absorber with continuously tunable stiffness [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(7): 1209-1224. |
| [3] | Meng LI, Hu DING. A vertical track nonlinear energy sink [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(6): 931-946. |
| [4] | Runqing CAO, Zilong GUO, Wei CHEN, Huliang DAI, Lin WANG. Nonlinear dynamics of a circular curved cantilevered pipe conveying pulsating fluid based on the geometrically exact model [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 261-276. |
| [5] | Jie JING, Xiaoye MAO, Hu DING, Liqun CHEN. Parametric resonance of axially functionally graded pipes conveying pulsating fluid [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(2): 239-260. |
| [6] | Hu DING, J. C. JI. Vibration control of fluid-conveying pipes: a state-of-the-art review [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1423-1456. |
| [7] | Jian ZANG, Ronghuan XIAO, Yewei ZHANG, Liqun CHEN. A novel way for vibration control of FGM fluid-conveying pipes via NiTiNOL-steel wire rope [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(6): 877-896. |
| [8] | Xin FAN, Changan ZHU, Xiaoye MAO, Hu DING. Adjacent mode resonance of a hydraulic pipe system consisting of parallel pipes coupled at middle points [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(3): 363-380. |
| [9] | Rongzhou LIN, Lei HOU, Yi CHEN, Yuhong JIN, N. A. SAEED, Yushu CHEN. A novel adaptive harmonic balance method with an asymptotic harmonic selection [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(11): 1887-1910. |
| [10] | Zilong GUO, Qiao NI, Wei CHEN, Huliang DAI, Lin WANG. Dynamic analysis and regulation of the flexible pipe conveying fluid with a hard-magnetic soft segment [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(9): 1415-1430. |
| [11] | Huliang DAI, Yixiang HE, Kun ZHOU, Zerui PENG, Lin WANG, P. HAGEDORN. Utilization of nonlinear vibrations of soft pipe conveying fluid for driving underwater bio-inspired robot [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(7): 1109-1124. |
| [12] | Guoxin JIN, Zhenghao WANG, Tianzhi YANG. Cascaded quasi-zero stiffness nonlinear low-frequency vibration isolator inspired by human spine [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(6): 813-824. |
| [13] | Hu DING, Yufei SHAO. NES cell [J]. Applied Mathematics and Mechanics (English Edition), 2022, 43(12): 1793-1804. |
| [14] | Wei CHEN, Ziyang HU, Huliang DAI, Lin WANG. Extremely large-amplitude oscillation of soft pipes conveying fluid under gravity [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(9): 1381-1400. |
| [15] | Zhong ZHANG, Muqing NIU, Kai YUAN, Yewei ZHANG. Research on linear/nonlinear viscous damping and hysteretic damping in nonlinear vibration isolation systems [J]. Applied Mathematics and Mechanics (English Edition), 2020, 41(7): 983-998. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS