Applied Mathematics and Mechanics (English Edition) ›› 2025, Vol. 46 ›› Issue (11): 2075-2094.doi: https://doi.org/10.1007/s10483-025-3318-9
Previous Articles Next Articles
Hongli LIU1,2, Shangchuan XIE3, Jie CHEN4,†( ), Fengming LI1, Wei ZHOU2
), Fengming LI1, Wei ZHOU2
Received:2025-07-14
Revised:2025-09-26
Published:2025-10-29
Contact:
†Jie CHEN, E-mail: jchen@bjut.edu.cnSupported by:2010 MSC Number:
Hongli LIU, Shangchuan XIE, Jie CHEN, Fengming LI, Wei ZHOU. Reduction of moving-load induced vibrations of graphene-reinforced composite beams with general boundary conditions viaa nonlinear energy sink. Applied Mathematics and Mechanics (English Edition), 2025, 46(11): 2075-2094.
Fig.?6
Effects of the spring stiffness on the nonlinear responses of beams with the GPL-U distribution: (a) translational spring stiffness with Kξ=104 N⋅m/rad and (b) torsional spring stiffness with Kz=1010 N/m, when kNES=1×107 N⋅m−3, cNES=40 N⋅m⋅s−1, r=200, f0=4 kN, and gGPL=0.5% (color online)"
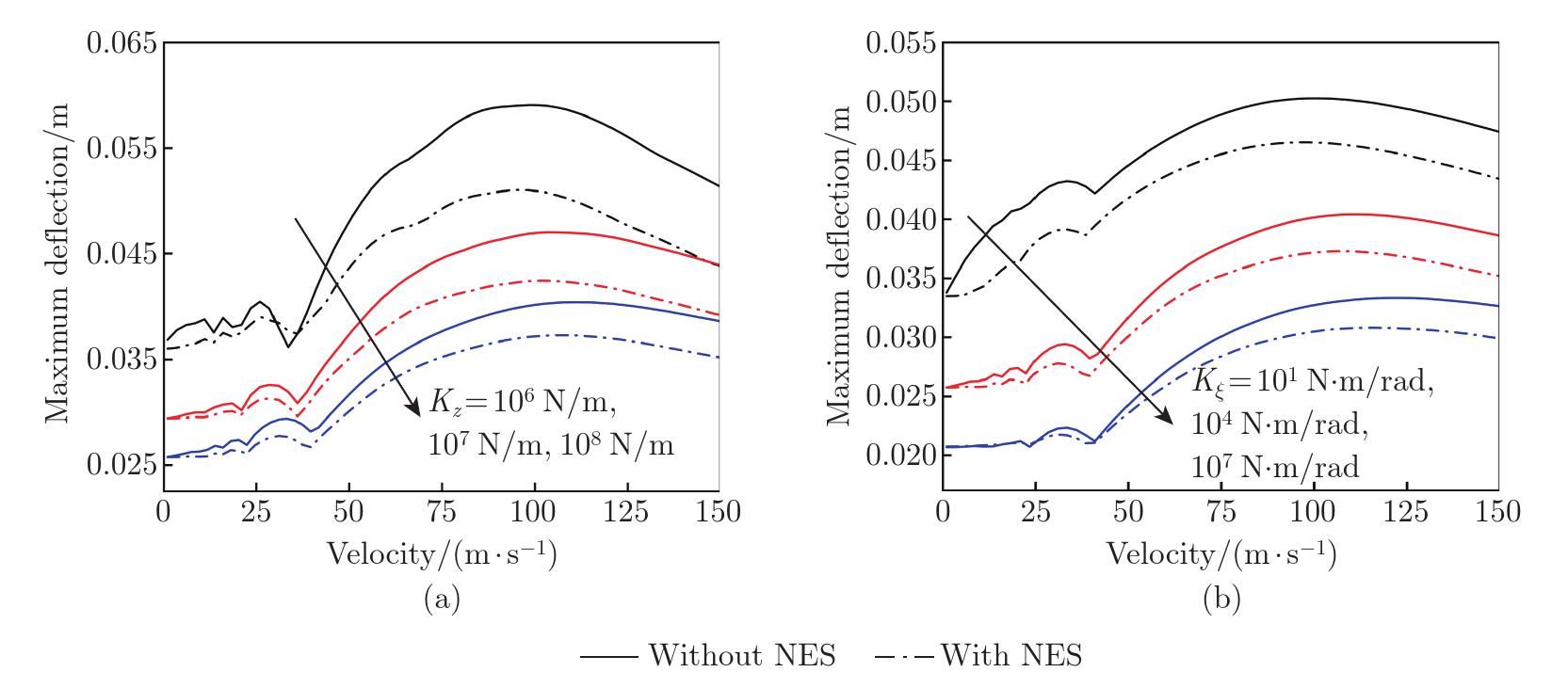
Fig.?7
Vibration reduction with the NES under different moving loads with the GPL-U distribution: (a) time history of beams at vf=60 m/s, (b) time history of beams at vf=100 m/s, (c) time-frequency response without the NES at vf=60 m/s, (d) time-frequency response with the NES at vf=60 m/s, (e) time-frequency response without the NES at vf=100 m/s, (f) time-frequency response with the NES at vf=100 m/s, when f0=4 kN, gGPL=0.5%, vf=100 m/s, Kz=106 N/m, and Kξ=104 N⋅m/rad (color online)"
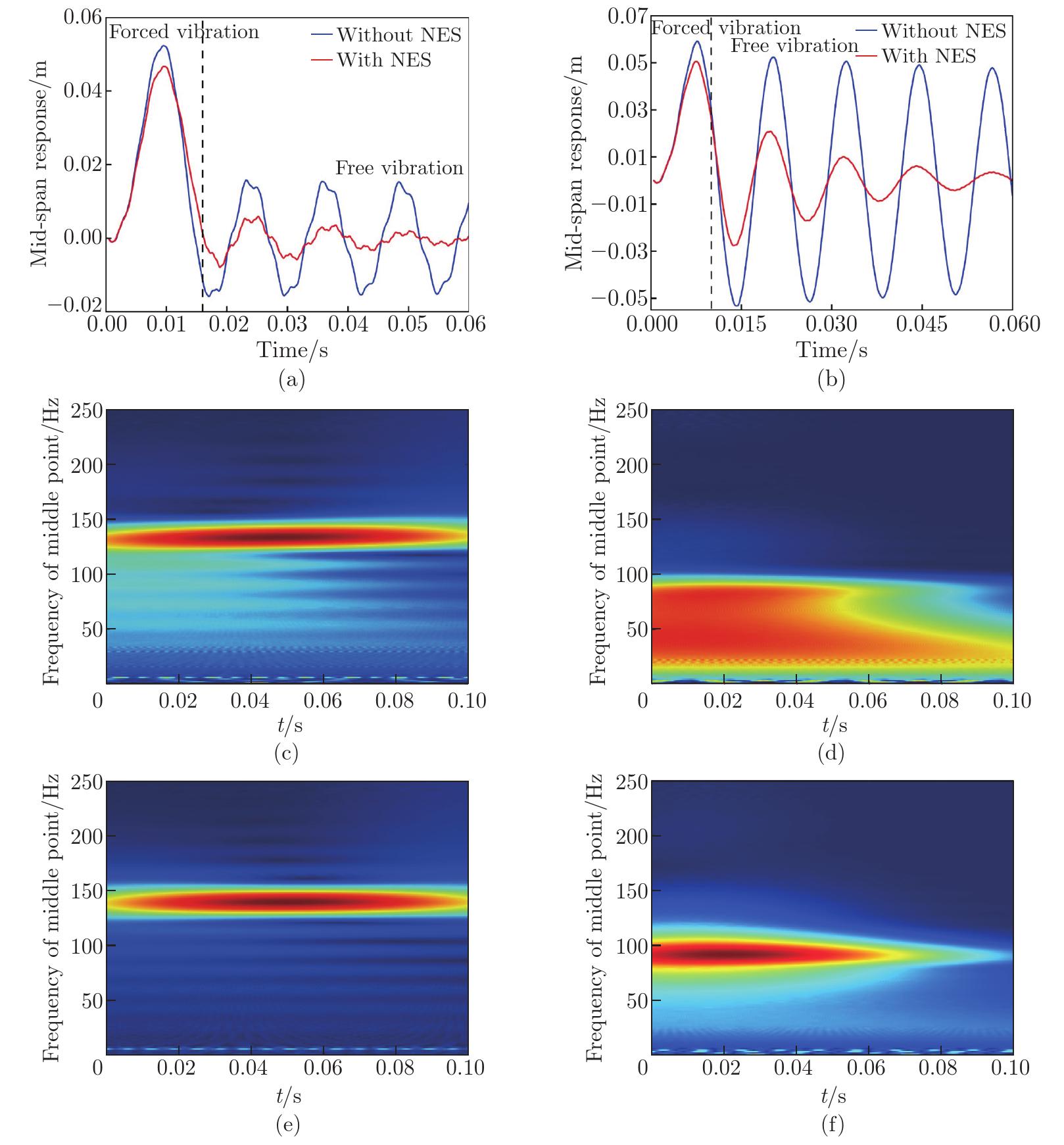
Fig.?11
Vibration reduction with the NES under different moving load frequencies with the GPL-U distribution: (a) time history of the beam at vf=10 m/s, (b) time history of the beam at vf=30 m/s, (c) time-frequency response without the NES at vf=10 m/s, (d) time-frequency response with the NES at vf=10 m/s, (e) time-frequency response without the NES at vf=30 m/s, and (f) time-frequency response with the NES at vf=30 m/s, when Kz=1010 N/m, Kξ=104 N⋅m/rad, f0=1 kN, and gGPL=0.5% (color online)"
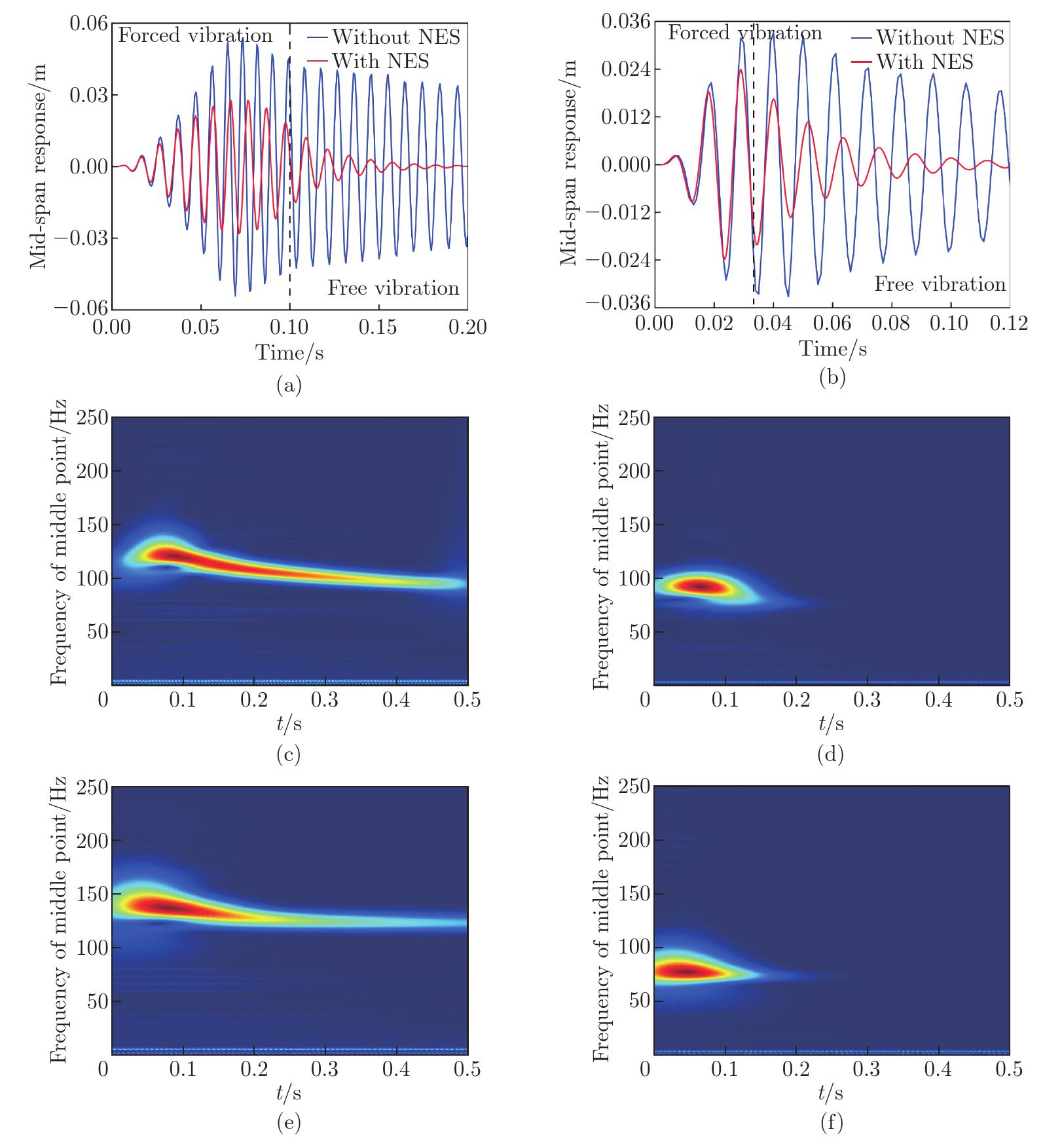

Fig.?12
Effects of the spring stiffness on the nonlinear response of GPL nanocomposite beams under moving harmonic loads with the GPL-U distribution: (a) translational spring stiffness with Kξ=104 N⋅m/rad and (b) torsional spring stiffness with Kz=1010 N/m, when gGPL=0.5%, f0=1 kN, and vf=10 m/s (color online)"
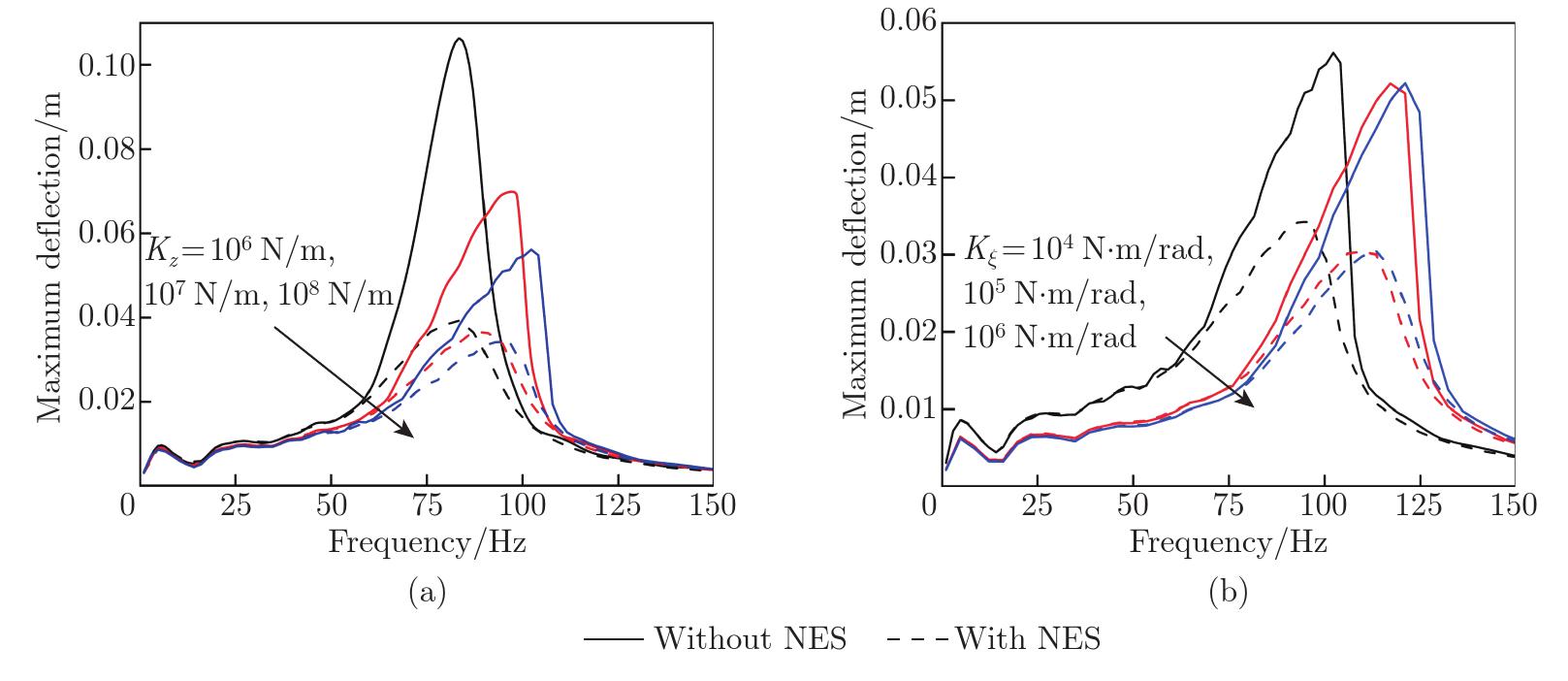
Fig.?13
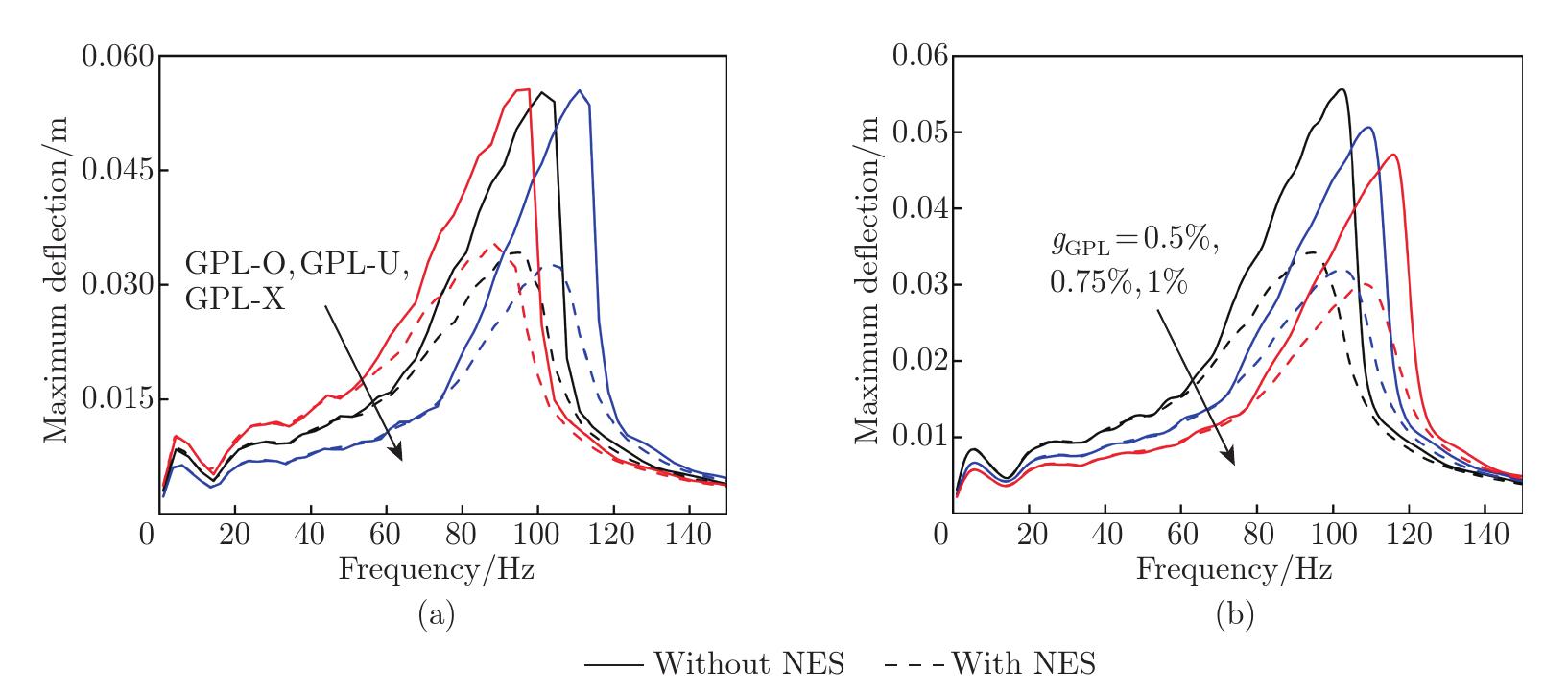
Nonlinear responses of FG-GPLRC beams under moving harmonic loading: (a) effect of the GPL distribution pattern, when f0=1 kN, gGPL=0.5%, Kz=1010 N/m, Kξ=104 N⋅m/rad, and vf=10 m/s and (b) effect of the GPL mass fraction with the GPL-U distribution, when f0=1 kN, Kz=1010 N/m, Kξ=104 N⋅m/rad, and vf=10 m/s (color online)"
| [1] | FRÝBA, L. Vibration of Solids and Structures under Moving Loads, Noordhoff Groningen, Netherlands (1972) |
| [2] | OUYANG, H. J. Moving-load dynamic problems: a tutorial (with a brief overview). Mechanical Systems and Signal Processing, 25(6), 2039–2060 (2011) |
| [3] | YANG, Y. B., YAU, J. D., URUSHDAZE, S., and LEE, T. Y. Historical review on resonance and cancellation of simply supported beams subjected to moving train loads: from theory to practice. International Journal of Structural Stability and Dynamics, 23, 2340008 (2023) |
| [4] | ŞIMŞEK, M. and AL-SHUJAIRI, M. Static, free and forced vibration of functionally graded (FG) sandwich beams excited by two successive moving harmonic loads. Composites Part B: Engineering, 108, 18–34 (2017) |
| [5] | WANG, Y. W., XIE, K., FU, T. R., and SHI, C. L. Vibration response of a functionally graded graphene nanoplatelet reinforced composite beam under two successive moving masses. Composite Structures, 209, 928–939 (2019) |
| [6] | SUN, H. and CHEN, J. Vibration reduction of graphene reinforced porous nanocomposite beams under moving loads using a nonlinear energy sink. Engineering Structures, 321, 118997 (2024) |
| [7] | SONG, M. T., KITIPORNCHAI, S., and YANG, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Composite Structures, 159, 579–588 (2017) |
| [8] | FENG, C., KITIPORNCHAI, S., and YANG, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Engineering Structures, 140, 110–119 (2017) |
| [9] | ZHAO, S. Y., ZHAO, Z., YANG, Z. C., KE, L. L., KITIPORNCHAI, S., and YANG, J. Functionally graded graphene reinforced composite structures: a review. Engineering Structures, 210, 110339 (2020) |
| [10] | KIANI, Y. Influence of graphene platelets on the response of composite plates subjected to a moving load. Mechanics Based Design of Structures and Machines, 50(4), 1123–1136 (2022) |
| [11] | ZHANG, W., MA, H., WANG, Y. B., and WANG, Y. W. Nonlinear transient thermo-mechanical responses of porous graphene platelet-reinforced cylindrical panels under moving distributed loads. Thin-Walled Structures, 192, 111180 (2023) |
| [12] | BAHRANIFARD, F., GOLBAHAR HAGHIGHI, M. R., and MALEKZADEH, P. In-plane responses of multilayer FG-GPLRC curved beams in thermal environment under moving load. Acta Mechanica, 231(7), 2679–2696 (2020) |
| [13] | MA, S. J., BAI, H. J., WANG, S. L., ZHAO, L., YANG, K., FANG, R., and ZHOU, X. Detecting the mass and position of a particle by the vibration of a cantilevered micro-plate. International Journal of Mechanical Sciences, 172, 105413 (2020) |
| [14] | XI, Y. Y., LYU, Q., ZHANG, N. H., and WU, J. Z. Thermal-induced snap-through buckling of simply-supported functionally graded beams. Applied Mathematics and Mechanics (English Edition), 41(12), 1821–1832 (2020) https://doi.org/10.1007/s10483-020-2691-7 |
| [15] | HE, F. F., DU, J. T., and LIU, Y. Dynamic behavior analysis of a spinning Timoshenko beam-rigid disk with nonlinear elastic boundaries under axial loading. Nonlinear Dynamics, 112, 2431–2452 (2024) |
| [16] | YE, S. Q., MAO, X. Y., DING, H., JI, J. C., and CHEN, L. Q. Nonlinear vibrations of a slightly curved beam with nonlinear boundary conditions. International Journal of Mechanical Sciences, 168, 105294 (2020) |
| [17] | CHEN, Q. and DU, J. T. A Fourier series solution for the transverse vibration of rotating beams with elastic boundary supports. Applied Acoustics, 155, 1–15 (2019) |
| [18] | QIAO, G. D. and RAHMATALLA, S. Influences of elastic supports on moving load identification of Euler-Bernoulli beams using angular velocity. Journal of Vibration and Acoustics, 143(4), 041010 (2021) |
| [19] | CHEN, H. Y., DING, H., LI, S. H., and CHEN, L. Q. Convergent term of the Galerkin truncation for dynamic response of sandwich beams on nonlinear foundations. Journal of Sound and Vibration, 483, 115514 (2020) |
| [20] | SHI, K., MO, X. Q., GAO, S. Y., YAO, H., and YANG, Y. B. General theory for damped beams with elastic supports subjected to a moving damped sprung mass. International Journal of Structural Stability and Dynamics, 25, 2550152 (2025) |
| [21] | WANG, Y. W., ZHOU, A. F., FU, T. R., and ZHANG, W. Transient response of a sandwich beam with functionally graded porous core traversed by a non-uniformly distributed moving mass. International Journal of Mechanics and Materials in Design, 16(3), 519–540 (2020) |
| [22] | WANG, Y. W. and WU, D. F. Thermal effect on the dynamic response of axially functionally graded beam subjected to a moving harmonic load. Acta Astronautica, 127, 171–181 (2016) |
| [23] | GENG, X. F., DING, H., WEI, K. X., and CHEN, L. Q. Suppression of multiple modal resonances of a cantilever beam by an impact damper. Applied Mathematics and Mechanics (English Edition), 41(3), 383–400 (2020) https://doi.org/10.1007/s10483-020-2588-9 |
| [24] | SAMANI, F. S. and PELLICANO, F. Vibration reduction on beams subjected to moving loads using linear and nonlinear dynamic absorbers. Journal of Sound and Vibration, 325(4-5), 742–754 (2009) |
| [25] | TIGLI, O. F. Optimum vibration absorber (tuned mass damper) design for linear damped systems subjected to random loads. Journal of Sound and Vibration, 331(13), 3035–3049 (2012) |
| [26] | VAKAKIS, A. F. Inducing passive nonlinear energy sinks in vibrating systems. Journal of Vibration and Acoustics, 123(3), 324–332 (2001) |
| [27] | XUE, J. R., ZHANG, Y. W., DING, H., and CHEN, L. Q. Vibration reduction evaluation of a linear system with a nonlinear energy sink under a harmonic and random excitation. Applied Mathematics and Mechanics (English Edition), 41(1), 1–14 (2020) https://doi.org/10.1007/s10483-020-2560-6 |
| [28] | ZHANG, Z., ZHANG, Y. W., and DING, H. Vibration control combining nonlinear isolation and nonlinear absorption. Nonlinear Dynamics, 100(3), 2121–2139 (2020) |
| [29] | DEKEMELE, K., DE KEYSER, R., and LOCCUFIER, M. Performance measures for targeted energy transfer and resonance capture cascading in nonlinear energy sinks. Nonlinear Dynamics, 93(2), 259–284 (2018) |
| [30] | FANG, X., WEN, J. H., YIN, J. F., and YU, D. L. Highly efficient continuous bistable nonlinear energy sink composed of a cantilever beam with partial constrained layer damping. Nonlinear Dynamics, 87(4), 2677–2695 (2017) |
| [31] | WANG, T. Z. and DING, Q. Targeted energy transfer analysis of a nonlinear oscillator coupled with bistable nonlinear energy sink based on nonlinear normal modes. Journal of Sound and Vibration, 556, 117727 (2023) |
| [32] | WANG, Y. F., KANG, H. J., CONG, Y. Y., GUO, T. D., and FU, T. Vibration suppression of a cable-stayed beam by a nonlinear energy sink. Nonlinear Dynamics, 111(16), 14829–14849 (2023) |
| [33] | ZHANG, M. J., WU, T., and ØISETH, O. Vortex-induced vibration control of a flexible circular cylinder using a nonlinear energy sink. Journal of Wind Engineering and Industrial Aerodynamics, 229, 105163 (2022) |
| [34] | SUN, H., CHEN, J., ZHANG, W., and LIU, D. K. Vibration suppression of Timoshenko beams subjected to moving loads using an inertial nonlinear energy sink. Acta Mechanica Sinica, 41, 524221 (2025) |
| [35] | CHANG, Z. Y., CHEN, J., and LI, Q. S. Vibration suppression for an elastically supported nonlinear beam coupled to an inertial nonlinear energy sink. International Journal of Structural Stability and Dynamics, 23(16-18), 2340017 (2023) |
| [36] | GENG, X. F., DING, H., JING, X. J., MAO, X. Y., WEI, K. X., and CHEN, L. Q. Dynamic design of a magnetic-enhanced nonlinear energy sink. Mechanical Systems and Signal Processing, 185, 109813 (2023) |
| [37] | CHEN, J. E., SUN, M., HU, W. H., ZHANG, J. H., and WEI, Z. C. Performance of non-smooth nonlinear energy sink with descending stiffness. Nonlinear Dynamics, 100(1), 255–267 (2020) |
| [38] | CHEN, J. N., ZHAO, J. Q., ZHANG, W., and SUN, M. Compound nonlinear energy sink with multiple motion types for absorbing energy from wide excitation ranges. Journal of Sound and Vibration, 617, 119273 (2025) |
| [39] | ZANG, J., YUAN, T. C., LU, Z. Q., ZHANG, Y. W., DING, H., and CHEN, L. Q. A lever-type nonlinear energy sink. Journal of Sound and Vibration, 437, 119–134 (2018) |
| [40] | DU, T. K., LIN, Y., JI, J. C., and DING, H. Series gravity-based track nonlinear energy sinks: design and experiment. Mechanical Systems and Signal Processing, 229, 112559 (2025) |
| [41] | ZHANG, Z., LU, Z. Q., DING, H., and CHEN, L. Q. An inertial nonlinear energy sink. Journal of Sound and Vibration, 450, 199–213 (2019) |
| [42] | CHEN, H. Y., ZENG, Y. C., DING, H., LAI, S., and CHEN, L. Q. Dynamics and vibration reduction performance of asymmetric tristable nonlinear energy sink. Applied Mathematics and Mechanics (English Edition), 45(3), 389–406 (2024) https://doi.org/10.1007/s10483-024-3095-9 |
| [43] | PARSEH, M., DARDEL, M., GHASEMI, M. H., and PASHAEI, M. H. Steady state dynamics of a non-linear beam coupled to a non-linear energy sink. International Journal of Non-Linear Mechanics, 79, 48–65 (2016) |
| [44] | SU, Z., JIN, G. Y., WANG, Y. L., and YE, X. M. A general Fourier formulation for vibration analysis of functionally graded sandwich beams with arbitrary boundary condition and resting on elastic foundations. Acta Mechanica, 227(5), 1493–1514 (2016) |
| [45] | KITIPORNCHAI, S., KE, L. L., YANG, J., and XIANG, Y. Nonlinear vibration of edge cracked functionally graded Timoshenko beams. Journal of Sound and Vibration, 324(3-5), 962–982 (2009) |
| [46] | SIMSEK, M. Non-linear vibration analysis of a functionally graded Timoshenko beam under action of a moving harmonic load. Composite Structures, 92(10), 2532–2546 (2010) |
| [1] | Peiliang ZHANG, Jianfei WANG. Macro fiber composite-based active control of nonlinear forced vibration of functionally graded plate [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(5): 869-884. |
| [2] | Youcheng ZENG, Hu DING, J. C. JI. An origami-inspired nonlinear energy sink: design, modeling, and analysis [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(4): 601-616. |
| [3] | Yuxin HAO, Lei SUN, Wei ZHANG, Han LI. Active traveling wave vibration control of elastic supported conical shells with smart micro fiber composites based on the differential quadrature method [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(2): 305-322. |
| [4] | Jie CHEN, Xinyue ZHANG, Mingyang FAN. Dynamic behaviors of graphene platelets-reinforced metal foam piezoelectric beams with velocity feedback control [J]. Applied Mathematics and Mechanics (English Edition), 2025, 46(1): 63-80. |
| [5] | Honglin WAN, Xianghong LI, Yongjun SHEN. Study on vibration reduction of two-scale system coupled with dynamic vibration absorber [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(8): 1335-1352. |
| [6] | Meng LI, Hu DING. A vertical track nonlinear energy sink [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(6): 931-946. |
| [7] | Hongyan CHEN, Youcheng ZENG, Hu DING, Siukai LAI, Liqun CHEN. Dynamics and vibration reduction performance of asymmetric tristable nonlinear energy sink [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(3): 389-406. |
| [8] | Jinxin DOU, Zhenping LI, Hongliang YAO, Muchuan DING, Guochong WEI. Torsional vibration suppression and electromechanical coupling characteristics of electric drive system considering misalignment [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(11): 1987-2010. |
| [9] | Jinhui LIU, Yu XUE, Zhihong GAO, A. O. KRUSHYNSKA, Jinqiang LI. Actively tunable sandwich acoustic metamaterials with magnetorheological elastomers [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(11): 1875-1894. |
| [10] | Jianing LIU, Jinqiang LI, Ying WU. Bandgap adjustment of a sandwich-like acoustic metamaterial plate with a frequency-displacement feedback control method [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1807-1820. |
| [11] | Jiawei MAO, Hao GAO, Junzhe ZHU, Penglin GAO, Yegao QU. Analytical modeling of piezoelectric meta-beams with unidirectional circuit for broadband vibration attenuation [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(10): 1665-1684. |
| [12] | Yong WANG, Peili WANG, Haodong MENG, Liqun CHEN. Dynamic performance and parameter optimization of a half-vehicle system coupled with an inerter-based X-structure nonlinear energy sink [J]. Applied Mathematics and Mechanics (English Edition), 2024, 45(1): 85-110. |
| [13] | Yang JIN, Tianzhi YANG. Enhanced vibration suppression and energy harvesting in fluid-conveying pipes [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1487-1496. |
| [14] | Hu DING, J. C. JI. Vibration control of fluid-conveying pipes: a state-of-the-art review [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(9): 1423-1456. |
| [15] | Shengtao ZHANG, Jiaxi ZHOU, Hu DING, Kai WANG, Daolin XU. Fractional nonlinear energy sinks [J]. Applied Mathematics and Mechanics (English Edition), 2023, 44(5): 711-726. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||


 Email Alert
Email Alert RSS
RSS